MathCAD — это просто! Часть 26. Продолжаем программировать в MathCAD
Как вы уже имели возможность убедиться благодаря статьям нашей серии, программирование в этой мощнейшей математической среде доступно всем начиная от старшеклассников и заканчивая академиками. Создатели MathCAD'а специально сделали средства программирования в ней достаточно простыми для того, кто не имеет опыта программирования на современных алгоритмических языках, поскольку таким людям тоже время от времени нужно писать небольшие программки в MathCAD'е.
Как вы помните, в прошлой статье мы с вами успели рассмотреть два небольших примера: в одном мы решали путем написания соответствующей программы квадратное уравнение, а во втором занимались аналогичным, в общем-то, образом транспонированием матриц. Что ж, эти примеры, безусловно, были весьма просты и наглядны, и с их помощью действительно вполне можно понять, каким именно образом действуют некоторые из тех операторов, которые я перечислил в самом начале нашего с вами разговора о программировании в MathCAD'е. Поэтому сегодня мы с вами продолжим заниматься написанием программ в этом замечательном математическом пакете, чтобы лучше разобраться во всех операторах, используемых в процессе программирования.
Еще немного о циклах: цикл while
В прошлый раз мы с вами уже пользовались понятием цикла, когда говорили о том, как работает наша программа, предназначенная для вычисления транспонированной матрицы по какой-то заранее заданной. Напомню, что в тот раз мы использовали цикл for, который, как я уже упоминал, имеет одну существенную отличительную особенность: он используется тогда, когда мы с вами уже заранее знаем, какое число итераций (повторений операций в цикле) должны будем совершить. Цикл for очень удобен именно своей предсказуемостью — поскольку мы заранее знаем, сколько у нас будет итераций, мы можем точно предугадать состояние каждой переменной во время каждой из итераций и не допустить ошибок, связанных с этими значениями. Однако, с другой стороны, такая предсказуемость этого цикла является и существенно отрицательной его стороной, поскольку очень и очень уменьшает его гибкость. Как нам быть, если мы заранее не знаем, когда нам остановить и прекратить наш цикл? Оказывается, для этой проблемы в MathCAD'е существует множество возможных вариантов решения, и, конечно же, мы с вами поговорим о каждом из них максимально подробным образом. Давайте напишем небольшую программу, которая будет заниматься суммированием элементов бесконечно убывающей геометрической прогрессии. Думаю, если не все, то по крайней мере большинство читателей этой статьи помнят (возможно, еще со школьной скамьи), что такая прогрессия является сходящимся рядом, а потому сумма всех ее элементов будет конечна. Конечно, разумно было бы для такого рода вычислений воспользоваться готовой формулой для вычисления суммы членов бесконечно убывающей геометрической прогрессии, которая, как и сама прогрессия, изучается еще в школе. Безусловно, если бы мы с вами не занимались изучением программирования, то именно так бы и поступили. Однако, поскольку мы все-таки разбираемся с программированием в среде MathCAD, то пойдем другим путем. Каким именно? Конечно же, мы напишем программу, которая будет путем простого суммирования вычислять интересующую нас сумму. Поскольку прогрессия хоть и убывающая, но, тем не менее, бесконечная, надо придумать какой-то критерий, который позволил бы нам все-таки завершить цикл. Дело в том, что, если мы будем вычислять цикл бесконечно, то со стороны будет казаться, что MathCAD просто завис, а потому никакого результата мы попросту не сможем дождаться. В таких случаях в качестве критерия завершения итерационного вычисления какого-либо значения обычно выбирают достижение членом прогрессии какого-либо достаточно малого значения, которое уже не будет влиять на результат.
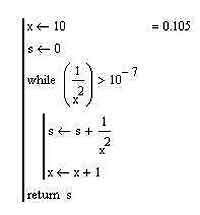Конечно, можно было бы заранее, зная вид нашей прогрессии, сказать, когда именно член прогрессии станет настолько малым, что мы перестанем замечать его вклад в общую сумму, и исходя из этого запланировать количество итераций для цикла for. Однако этот вариант, скажем прямо, конструктивным назвать ни язык не поворачивается, ни рука не поднимается. Если воспользоваться не for, а другим видом цикла, не требующим от нас заранее указывать число итераций, то мы убьем сразу двух зайцев. Во-первых, нам не потребуется ничего заранее вычислять — MathCAD сам посчитает все, что ему будет нужно, в процессе выполнения написанной нами программы. Во-вторых, мы получим универсальную программу, которая может работать с любой бесконечно убывающей последовательностью — для этого не потребуется по-новой вычислять количество необходимых итераций; достаточно будет изменить одну-единственную формулу во всем тексте программы. Итак, давайте же посмотрим, наконец, на этот самый текст, а затем его немного обсудим.
Здесь x, как несложно, в общем-то, догадаться, та самая переменная, которая служит для обозначения номера элемента нашей прогрессии, а s содержит в себе значение суммы ее членов. x-й член нашей прогрессии вычисляется по формуле 1/x2, а суммировать такие члены наша программа должна будет до тех пор, пока их значение не станет меньше, чем 10-7. Как показывает практика, для того, чтобы вычислить сумму с точностью до трех знаков после запятой, такого ограничения вполне достаточно. Для организации цикла с заранее неизвестным числом итераций мы использовали оператор while. Он будет выполнять наш цикл до тех пор, пока условие, записанное после ключевого слова while, не станет ложным. Обратите внимание, что для того, чтобы записать внутри цикла больше одной строки программного кода, нам нужно, чтобы был отступ влево, обозначенный второй черной линией. Также здесь можно увидеть операторы присваивания, о которых я говорил в прошлый раз. Конструкция x < x +1 используется для увеличения значения переменной x на единицу в каждом шаге цикла, а s < s + 1/x2 — для увеличения значения переменной s на величину 1/x2.
Управление ходом выполнения циклов: оператор break
Когда я говорил о том, что записать программу для вычисления суммы членов бесконечно убывающей геометрической прогрессии можно только в том случае, если мы предварительно рассчитаем число итераций, я немного лукавил. "Как же так? — можете спросить вы. — Значит, цикл for вовсе не обязательно подразумевает априорное знание числа необходимых итераций?" Подразумевает, однако это вовсе не означает, что мы обязательно должны указывать именно то число, которое потребуется для достижения указанной точности. Мы можем указать заведомо большее число итераций, а при достижении некоторого минимального значения x-го члена прогрессии просто прервать выполнение цикла. MathCAD позволяет нам сделать такой финт ушами, потому что существует специальная конструкция для прерывания цикла — это оператор break. Давайте посмотрим, каким образом будет выглядеть наша программа для вычисления суммы членов бесконечно убывающей геометрической прогрессии, записанная с использованием цикла for и оператора break.
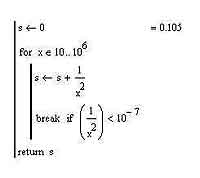Как видите, все действительно очень просто — поскольку цикл for мы с вами уже вроде как изучили, то особенно заострять внимание на нем не буду. Оператор break прерывает выполнение цикла, и выполнение программы продолжается со строки, следующей непосредственно за циклом. Ну, или, если такой строки нет, то на этом оно, в общем-то, и заканчивается. Оператор break можно применять не только в цикле for, но и в цикле while, хотя во втором из них он, конечно же, применяется реже. Конечно, такой способ реализации вычислений в том случае, если число итераций заранее неизвестно, не отличается особым изяществом, однако, коль скоро он также существует, стало быть, его не зря придумали, и будет достаточно полезно иметь его в виду. На самом деле, конечно, в таких ситуациях лучше пользоваться циклом while, поскольку оператор break придуман для совершенно иных случаев. Каких именно? Дело в том, что иногда невозможно выбрать только одно условие завершения цикла, а потому, чтобы не загромождать заголовок цикла while, а также в цикле for, где условие и вовсе указать никак иначе попросту нельзя, используют именно оператор break. Думаю, если вы будете писать программы в MathCAD для решения каких-либо более жизненных задач, то вы рано или поздно столкнетесь с необходимостью применения этого полезного оператора.
Управление ходом выполнения циклов: оператор continue
Есть и еще один оператор управления ходом выполнения циклов, и именно о нем мы с вами поговорим напоследок в этой статье. Дело в том, что не всегда бывает необходимым прекратить выполнение цикла вообще — иногда нужно просто перескочить с текущей итерации сразу на следующую, не прекращая при этом выполнения самого цикла. Специально для таких случаев создатели MathCAD'а предусмотрели не менее полезный оператор continue. В качестве примера давайте рассмотрим знакочередующуюся последовательность. Представим, что перед нами стоит задача найти с заданной точностью сумму только ее нечетных (отрицательных) членов. Вот как, таким образом, может выглядеть решение поставленной перед нами задачи.
Как видите, здесь вполне можно было бы обойтись и без оператора continue — например, если непосредственно перед увеличением значения суммы проверять знак слагаемого. Однако, поскольку нам с вами нужно было посмотреть, как этот оператор действует на практике, я решил написать программу именно в таком варианте. Кроме оператора continue, все остальное, в принципе, вам должно быть знакомо — единственное, что стоит отметить, — это функция sign. Она возвращает -1, если знак ее аргумента меньше нуля, 1 — если больше нуля, и 0 — если равен нулю.
Выводы
Что ж, давайте, пожалуй, подытожим все то, что было сказано нами ранее. Как видите, в MathCAD есть очень много мощных и гибких средств построения циклов — не обязательно использовать требующую зачастую слишком многого конструкцию for, когда есть возможность использовать while. Кроме того, благодаря операторам break и continue управлять циклами можно на принципиально новом уровне, вмешиваясь в работу цикла на каждом шаге каждой итерации, если вдруг возникнет такая необходимость.
Конечно, для того, чтобы грамотно использовать все те конструкции, о которых мы с вами сейчас здесь поговорили, требуется опыт. Приобрести его можно, конечно же, регулярными упражнениями в мощной математической среде MathCAD, которые доступны каждому из наших читателей. Если регулярно практиковаться, поверьте, работа в MathCAD будет не простой, а очень простой.
SF, spaceflyer@tut.by
Как вы помните, в прошлой статье мы с вами успели рассмотреть два небольших примера: в одном мы решали путем написания соответствующей программы квадратное уравнение, а во втором занимались аналогичным, в общем-то, образом транспонированием матриц. Что ж, эти примеры, безусловно, были весьма просты и наглядны, и с их помощью действительно вполне можно понять, каким именно образом действуют некоторые из тех операторов, которые я перечислил в самом начале нашего с вами разговора о программировании в MathCAD'е. Поэтому сегодня мы с вами продолжим заниматься написанием программ в этом замечательном математическом пакете, чтобы лучше разобраться во всех операторах, используемых в процессе программирования.
Еще немного о циклах: цикл while
В прошлый раз мы с вами уже пользовались понятием цикла, когда говорили о том, как работает наша программа, предназначенная для вычисления транспонированной матрицы по какой-то заранее заданной. Напомню, что в тот раз мы использовали цикл for, который, как я уже упоминал, имеет одну существенную отличительную особенность: он используется тогда, когда мы с вами уже заранее знаем, какое число итераций (повторений операций в цикле) должны будем совершить. Цикл for очень удобен именно своей предсказуемостью — поскольку мы заранее знаем, сколько у нас будет итераций, мы можем точно предугадать состояние каждой переменной во время каждой из итераций и не допустить ошибок, связанных с этими значениями. Однако, с другой стороны, такая предсказуемость этого цикла является и существенно отрицательной его стороной, поскольку очень и очень уменьшает его гибкость. Как нам быть, если мы заранее не знаем, когда нам остановить и прекратить наш цикл? Оказывается, для этой проблемы в MathCAD'е существует множество возможных вариантов решения, и, конечно же, мы с вами поговорим о каждом из них максимально подробным образом. Давайте напишем небольшую программу, которая будет заниматься суммированием элементов бесконечно убывающей геометрической прогрессии. Думаю, если не все, то по крайней мере большинство читателей этой статьи помнят (возможно, еще со школьной скамьи), что такая прогрессия является сходящимся рядом, а потому сумма всех ее элементов будет конечна. Конечно, разумно было бы для такого рода вычислений воспользоваться готовой формулой для вычисления суммы членов бесконечно убывающей геометрической прогрессии, которая, как и сама прогрессия, изучается еще в школе. Безусловно, если бы мы с вами не занимались изучением программирования, то именно так бы и поступили. Однако, поскольку мы все-таки разбираемся с программированием в среде MathCAD, то пойдем другим путем. Каким именно? Конечно же, мы напишем программу, которая будет путем простого суммирования вычислять интересующую нас сумму. Поскольку прогрессия хоть и убывающая, но, тем не менее, бесконечная, надо придумать какой-то критерий, который позволил бы нам все-таки завершить цикл. Дело в том, что, если мы будем вычислять цикл бесконечно, то со стороны будет казаться, что MathCAD просто завис, а потому никакого результата мы попросту не сможем дождаться. В таких случаях в качестве критерия завершения итерационного вычисления какого-либо значения обычно выбирают достижение членом прогрессии какого-либо достаточно малого значения, которое уже не будет влиять на результат.
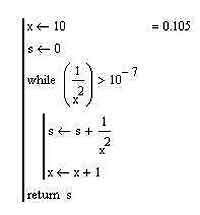
Здесь x, как несложно, в общем-то, догадаться, та самая переменная, которая служит для обозначения номера элемента нашей прогрессии, а s содержит в себе значение суммы ее членов. x-й член нашей прогрессии вычисляется по формуле 1/x2, а суммировать такие члены наша программа должна будет до тех пор, пока их значение не станет меньше, чем 10-7. Как показывает практика, для того, чтобы вычислить сумму с точностью до трех знаков после запятой, такого ограничения вполне достаточно. Для организации цикла с заранее неизвестным числом итераций мы использовали оператор while. Он будет выполнять наш цикл до тех пор, пока условие, записанное после ключевого слова while, не станет ложным. Обратите внимание, что для того, чтобы записать внутри цикла больше одной строки программного кода, нам нужно, чтобы был отступ влево, обозначенный второй черной линией. Также здесь можно увидеть операторы присваивания, о которых я говорил в прошлый раз. Конструкция x < x +1 используется для увеличения значения переменной x на единицу в каждом шаге цикла, а s < s + 1/x2 — для увеличения значения переменной s на величину 1/x2.
Управление ходом выполнения циклов: оператор break
Когда я говорил о том, что записать программу для вычисления суммы членов бесконечно убывающей геометрической прогрессии можно только в том случае, если мы предварительно рассчитаем число итераций, я немного лукавил. "Как же так? — можете спросить вы. — Значит, цикл for вовсе не обязательно подразумевает априорное знание числа необходимых итераций?" Подразумевает, однако это вовсе не означает, что мы обязательно должны указывать именно то число, которое потребуется для достижения указанной точности. Мы можем указать заведомо большее число итераций, а при достижении некоторого минимального значения x-го члена прогрессии просто прервать выполнение цикла. MathCAD позволяет нам сделать такой финт ушами, потому что существует специальная конструкция для прерывания цикла — это оператор break. Давайте посмотрим, каким образом будет выглядеть наша программа для вычисления суммы членов бесконечно убывающей геометрической прогрессии, записанная с использованием цикла for и оператора break.
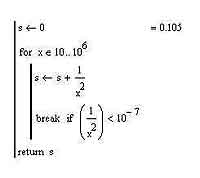
Управление ходом выполнения циклов: оператор continue
Есть и еще один оператор управления ходом выполнения циклов, и именно о нем мы с вами поговорим напоследок в этой статье. Дело в том, что не всегда бывает необходимым прекратить выполнение цикла вообще — иногда нужно просто перескочить с текущей итерации сразу на следующую, не прекращая при этом выполнения самого цикла. Специально для таких случаев создатели MathCAD'а предусмотрели не менее полезный оператор continue. В качестве примера давайте рассмотрим знакочередующуюся последовательность. Представим, что перед нами стоит задача найти с заданной точностью сумму только ее нечетных (отрицательных) членов. Вот как, таким образом, может выглядеть решение поставленной перед нами задачи.
Выводы
Что ж, давайте, пожалуй, подытожим все то, что было сказано нами ранее. Как видите, в MathCAD есть очень много мощных и гибких средств построения циклов — не обязательно использовать требующую зачастую слишком многого конструкцию for, когда есть возможность использовать while. Кроме того, благодаря операторам break и continue управлять циклами можно на принципиально новом уровне, вмешиваясь в работу цикла на каждом шаге каждой итерации, если вдруг возникнет такая необходимость.
Конечно, для того, чтобы грамотно использовать все те конструкции, о которых мы с вами сейчас здесь поговорили, требуется опыт. Приобрести его можно, конечно же, регулярными упражнениями в мощной математической среде MathCAD, которые доступны каждому из наших читателей. Если регулярно практиковаться, поверьте, работа в MathCAD будет не простой, а очень простой.
SF, spaceflyer@tut.by
Компьютерная газета. Статья была опубликована в номере 40 за 2008 год в рубрике soft
