Статьи из номера 2007/27
Звук: вопрос — ответ
2007/27‣мультимедиа
Приветствую вас, уважаемые… Просто вы в письмах здороваетесь, вот и я решил. Кто не понял, это было вступление. Приступим… С большим удовольствием читаю ваши статьи в КГ. И вы стали для меня авторитетом в области звука. Я учусь по специальности, со звуком никак не связанной, но он стал моей жизнью, без преувеличения. Этим заниматься я начал два года назад с программки ReBirth. Сейчас пытаюсь сам писать музыку, ремиксовать, сводить — я имею в ... подробнее
IT-индустрия: история Alcatel
2007/27‣бизнес
Брэнд Alcatel хорошо знаком нашим потребителям. Но, в отличие от Siemens, Panasonic, Samsung и прочих гигантов, на постсоветском пространстве компания Alcatel известна в основном своими сотовыми телефонами. И мало кто у нас знает, что на самом деле производство мобильных телефонов — это скорее побочный бизнес для французского телекоммуникационного гиганта. Французская душа коммуникаций Безо всякой задней рекламной мысли должен заметить: ... подробнее
В поисках домашнего универсала. Монитор Samsung SynsMaster 940Fn
2007/27‣hard

Не секрет, что подавляющее большинство продаваемых сегодня компьютеров комплектуются LCD-мониторами. Ассортимент продукции очень богат, модельный ряд обновляется быстро - каждый производитель мониторов пытается отхватить свой кусок "пирога", гибко подстраиваясь под конъюнктуру рынка. И если совсем недавно "правили бал" 17" модели, то сейчас на рынке "бюджетных" мониторов лидерство переходит к аппаратам с диагональю в 19 дюймов. К сожалению, ... подробнее
Дорога из желтого кирпича: строим пользовательские интерфейсы вместе с Flash 9 & ASWing. Часть 3
2007/27‣программирование
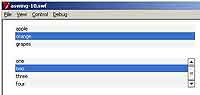
Сегодня мы продолжим знакомство с библиотекой визуальных элементов управления ASWing3. Мы научимся работать со сложными элементами — такими, как падающие списки, таблицы. Также мы на примерах разберем концепцию MVC, с использованием которой и построена данная библиотека. Что такое MVC? Вкратце это технология проектирования/программирования, продолжающая идею "Разделяй и властвуй". Сделав части программы максимально независимыми друг от друга ... подробнее
DARPA LANdroids: грант на $1 млн
2007/27‣робототика
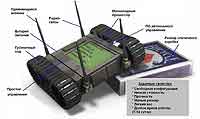
В новостных лентах очень часто можно запутаться. Например, о LAN-дроидах стали писать, как будто они уже созданы или вот-вот будут созданы. На самом деле это далеко не так. Проект является стартующим. Известное всем подразделение министерства обороны США — агентство DARPA (The Defense Advanced Research Projects Agency) — объявило конкурс на разработки для нового проекта, имеющего название LANdroids. Он подразумевает создание небольших ... подробнее
Память от Team Group: Elite и Value, или Кто на новенького?
2007/27‣hard

Так уж повелось, что IT-индустрия является самой быстроразвивающейся отраслью промышленности. Причем в данный момент мы говорим не столько о технической стороне вопроса, сколько о коммерческой. Появляются новые компании, разоряются старые, создаются союзы, происходят поглощения слабых сильными... И все это происходит невероятно для столь высокотехнологичной индустрии быстро и динамично. Вот и сегодня нам предстоит познакомиться с новым, для ... подробнее
Простая навигация 3: Mio DigiWalker P550
2007/27‣mobile
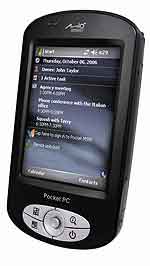
Спутниковая навигация становится все более популярной в странах СНГ. Во многом это происходит потому, что ассортимент карманных компьютеров со встроенным GPS-модулем и GPS-навигаторов ощутимо расширился за последние годы. В результате здоровой конкуренции снизилась и цена на такие устройства. Расширилась также функциональность этих наладонников — в них начали встраивать Bluetooth и Wi-Fi.Сегодня я хочу рассказать о Mio DigiWalker P550 — ... подробнее
Рисуем бороду
2007/27‣soft

В то время, как большинство людей стремятся избавиться от лишних волос, в век эпиляции, бритв и т.п. в моей голове родился данный урок. Согласитесь, ведь иногда грамотно обработанные волосы могут послужить неплохим элементом стиля. Поначалу, чтобы скрыть возможные недоработки в имидже, я хотел взять фотографию девушки, но, подумав немного, решил отказаться:). Шаг 1 Итак, для того, чтобы нарисовать дополнительный волосяной покров, нам ... подробнее
Google Experimental: новые инструменты поиска
2007/27‣soft

КГ неоднократно обращалась к тематике эффективного поиска с помощью Google. Очередной повод вспомнить об этой компании и принадлежащему ей интернет-поисковику дал запуск на известном ресурсе Google Labs нового раздела, посвященного поискам в области развития пользовательского интерфейса. Такие новинки в перспективе могут затронуть всех многочисленных пользователей Google. Давайте пройдемся по проектам Google Experimental и попробуем ... подробнее
Video Pilot 1.21
2007/27‣soft

сайт 4,9 Мб shareware/demo Компания Two Pilots известна главным образом благодаря своему продукту Color Pilot — удобному средству корректировки цветов на отсканированных и отснятых изображениях, доступному также в виде плагина для Photoshop. Не все знают, что, помимо продукта, ориентированного на работу с изображениями, разработчики создали и аналогичное решение для видео. Так что знакомьтесь: Video Pilot. С его помощью видеоролики, ... подробнее
Bersirc 2.2
2007/27‣soft
сайт 0,2 Мб freeware/open source Минималистичный и очень легкий клиент IRC с открытым исходным кодом. Даже в установленном виде программа занимает меньше 400 Кб! Работа с Bersirc достаточно проста: после ввода информации о пользователе (ник, реальное имя, username — доступно использование нескольких таких профилей), просто укажите, к какому серверу подключиться, и, если нужно, пароль. Вуаля! Правда, в отличие других популярных клиентов ... подробнее
Map Designer 2.22 Pro
2007/27‣soft
сайт 1,1 Мб shareware/trialware ($25) Полезная программа для веб-дизайнеров, позволяющая создавать так называемые карты изображений (image maps). Если кто-то из читателей не в курсе, что это такое, вспомните: наверняка хоть один раз в жизни, а скорее всего, куда чаще, вы видели сайт(ы), где на одном изображении находилось несколько (или одна, но не захватывающая всю картинку) зон, на которые были повешены гиперссылки? Простейший пример — ... подробнее
Мыши ModeCom MC-212 и MC-802. Меняем стандарты
2007/27‣hard

Случаи, когда производители предпринимают попытки завоевать внимание рядового потребителя, в последнее время происходят все чаще. Как правило, это делается двумя способами: с помощью супероригинального дизайна с экзотическими технологическими наворотами или банального снижения цен на свою продукцию. Однако бывает и так, что оба этих способа умудряются сочетать в одном и том же устройстве, что уже само по себе делает его уникальным. Одним, а ... подробнее
Flash-MP3-плейер JAGGA BOOM B1002
2007/27‣hard

Сегодня умение проигрывать музыкальные файлы формата МР3 производители встраивают во все, где это могло бы быть хоть как-либо уместно: DVD- проигрыватели, мобильные телефоны, наручные часы, и даже… солнцезащитные очки. Осталось дождаться только, когда "запоют" цифровые фотокамеры. Там ведь тоже есть Flash-память, не так ли? Однако, несмотря на преогромное количество моделей простейших MP3-плейеров, в список возможностей которых, помимо ... подробнее
Тест корпуса Foxconn TLA-436: сборка ПК в рамках бюджета
2007/27‣hard

Вопрос выбора корпуса для сборки компьютера всегда является довольно важным и непростым как для неопытных пользователей, так и для профессионалов. Ситуация усугубляется вдвойне, если требуется построить качественную систему с минимальными вложениями. Во-первых, желательно подобрать корпус с хорошим комплектным блоком питания, чтобы избежать дополнительных вложений. Во-вторых, требуется позаботиться об оптимальном размещении ваших ... подробнее
Тестирование блока питания HIPER HPU-4M530-PU V1 среднего ценового диапазона
2007/27‣hard

Как правило, в своих обзорах единичных продуктов, посвященных блокам питания для ПК, мы рассматриваем топовые решения от различных производителей. Данные БП наиболее интересны в плане изучения, так как применяются продвинутые методы разработки, однако в реальной жизни все немного иначе. Вспомните: у кого в домашнем компьютере установлен источник стоимостью €100 и выше? Правильно: обычные пользователи по понятным причинам предпочитают бюджетные ... подробнее


