Flash 8 & Физика. Введение
Для меня большой интерес представляет наблюдать за тем, что происходит на стыке двух разных технологий, и чем более разные и непохожие эти подходы, тем более интересные могут получаться результаты. Сегодня мы попробуем смешать средства flash 8 и несколько простых законов физики. Тема сегодняшнего материала более ориентирована на разработчиков flash-игр, но базовые идеи могут быть применены и для смежных задач — например, создание обучающих flash-роликов по физике или математике.
Разумеется, физика и flash и должны были быть с самого начала едиными. Но из-за очевидных причин разработчики macromedia не создали в составе flash развитых библиотек или наборов функций, которые позволяли бы моделировать окружающий нас физический мир. В самом начале пути flash это могло быть оправдано общей примитивностью языка actionscript и нежеланием повышать требования к профессиональному уровню дизайнеров. Но когда появился actionscript2 и тем более flex|mxml|actionscript3, когда в мир flash потянулись более программисты, чем дизайнеры, они могут позволить себе более не довольствоваться примитивными продуктами от macromedia|adobe, а разработать собственные средства, взяв идеи из мира java|smalltalk|eclipse|xaml. Когда я думал над конкретным наполнением сегодняшнего материала, во мне боролись два желания. Первое — рассказать о новых инструментах и библиотеках, которые разработало сообщество (не adobe) и которые ориентируются на actionscript3|flex и будущий flash9. Или же отложить этот материал до лучших времен и рассказать о том, как быть тем, кто работает с flash8. В общем, вторая идея победила. Я предполагаю, что вы умеете хоть как-то работать с flash8 и еще не совсем забыли школьный курс математики.
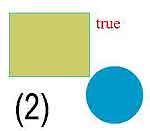Сначала рассмотрим стандартные средства flash, предусмотренные его разработчиками. К сожалению, они настолько примитивны и ограничены, что рассмотрение их возможностей не займет много времени. Для определения, произошло ли столкновение двух объектов клипов, а также для проверки, попадает ли некоторая точка (в простейшем случае — курсор мыши) в область определенного клипа, служит метод hitTest. Есть два базовых приема его использования. Первый предполагает вызов метода hitTest от имени некоторого объекта со следующими параметрами: координата_x, координата_y, принцип проверки. Метод hitTest вернет вам значение "true" в случае, если точка лежит внутри данного объекта. Третий параметр метода hitTest управляет тем, как именно будет выполняться проверка попадания точки внутрь фигуры. Очевидно, что для ряда фигур проверка того, лежит ли в них точка, достаточно нетривиальна. Поэтому, если третий параметр равен true, то выполняется точная проверка, иначе вокруг фигуры рисуется воображаемая рамка окружающего фигуру прямоугольника, и точка проверяется на попадание внутрь не фигуры, а, именно описывающего прямоугольника (bounding box). Для примера создайте три клипа с именами smb1, smb2, smb3 — это будут фигуры соответственно прямоугольника, круга и некоторой кривой. Дайте экземплярам клипов, расположенных на слое layer1, имена smb1_obj, smb3_obj и smb3_obj. Сделайте так, чтобы прямоугольник и круг частично пересекались и имели общую область. Также я разместил на слое компонент checkbox с именем chk_if_shape. Затем в первый кадр слоя layer1 введите следующий код:
this.createTextField("status_txt", 999, 0, 0, 400, 22);
var mouseListener:Object = new Object();
mouseListener.onMouseMove = function():Void {
status_txt.text =
" layer0: " + _level0.hitTest(_xmouse, _ymouse, true) +
" object 1: " + _root.smb1_obj.hitTest(_xmouse, _ymouse, _root.chk_if_shape.selected) +
" object 2: " + _root.smb2_obj.hitTest(_xmouse, _ymouse, _root.chk_if_shape.selected) +
" object 3: " + _root.smb3_obj.hitTest(_xmouse, _ymouse, _root.chk_if_shape.selected)
;
}
Mouse.addListener(mouseListener);
В примере выше я создаю текстовую надпись с именем status_txt. Она будет служить для вывода сообщений из созданного ниже объекта-слушателя на событие перемещение мыши. Каждый раз внутри данного обработчика я вызываю метод hitTest с координатами мыши, а также с признаком того, отмечен или нет checkbox, влияющий на алгоритм расчета попадания точки внутрь фигуры. При вызове hitTest от имени "_layer0" я проверяю, попала ли мышь внутрь какого-либо объекта вообще. Поперемещайте мышь и посмотрите, что будет происходить, когда курсор находится внутри фигуры 3, или же когда курсор находится не внутри круга, но в пределах описывающего его квадрата, и как на это влияет отметка checkbox. Второй возможный способ использования метода hitTest — это проверка того, соприкасаются ли два объекта между собой. Для демонстрации я взял пример из справки flash8, только немного его дополнил — так, чтобы показать не самые приятные стороны этой функции. Итак, создайте два объекта клипа: прямоугольник smb_box и круг smb_circle. Затем на слое layer1 разместите по экземпляру этих клипов с именами соответственно smb_box_obj и smb_circle_obj. Рядом с ними я разместил объект динамического текста с именем txt_status. В первый кадр слоя внесите следующий код. Вкратце в нем я добавил поддержку перетаскивания мышью объекта круга, а для объекта прямоугольника добавил постоянную проверку, соприкасаются ли эти две фигуры между собой, с выводом результатов в текстовое поле txt_status.
smb_box_obj.onEnterFrame = function() {
_root.txt_status.text = this.hitTest(smb_circle_obj);
};
smb_circle_obj.onPress = function() {
this.startDrag(false);
updateAfterEvent();
};
smb_circle_obj.onRelease = function() {
this.stopDrag();
};
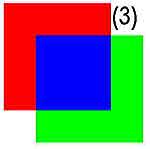
Результат работы виден на картинке 2. Обратите внимание на то, что надпись txt_status отмечает значение true (фигуры пересекаются) еще в тот момент, когда этого соприкосновения еще нет. На самом деле hitTest работает так: вокруг объектов рисуются ограничивающие их прямоугольники, и проверяется, не пересекаются ли сами фигуры, а именно: пересекаются ли ограничивающие их прямоугольники. Может быть, macromedia предусмотрела еще какие-то методы анализа. Увы, нет. Мы не можем не только точно определить, столкнулись ли два объекта, но и их дальнейшее поведение. Фактически если вы делаете игрушку, то создаете ее как набор жестко предопределенных сценариев поведения. Скажем, в гоночках, если машинка соприкоснулась с другой машинкой, она получает повреждения и отскакивает в сторону. Но является ли расчет количества повреждений и траектории отскока зависящим от того, как именно соприкоснулись эти два объекта? Были ли их траектории касательными, или же было лобовое столкновение? Боюсь, вам придется написать очень много проверок возможных ситуаций, если будете пользоваться подаренным macromedia методом hitTest. Так что придется нам, вооружившись отнятым у младшего брата или сестренки учебником по физике, реализовать пару алгоритмов самим. К счастью, задачи обнаружения пересечения объектов не только сложны, но и давно изучены.
Весь дальнейший материал ориентируется на 2d пространство. Методы работы с 3d во flash будут рассмотрены позже при условии появления откликов от читателей. Итак, процесс обнаружения того, соприкоснулись ли и как два объекта, начинается со стадии, когда определяется, какие пары объектов могут соприкоснуться (broad phase). Так, если у вас в сцене 100 объектов, то глупо перебивать все пары 100*100-1=9999 и запускать для каждой из них довольно трудоемкий алгоритм, определяющий конкретные детали такого соприкосновения. Для упрощенной проверки соприкосновения объектов мы создаем вокруг них bounding box (так же, как делает метод hitTest), а затем проверяем, пересекаются ли данные прямоугольники. Начиная с flash8 за это отвечает класс flash.geom.Rectangle. Если у вас фигура задается в общем случае некоторым полигоном, то вам нужно найти крайние точки: максимальные и минимальные координаты среди всех вершин полигона.
// импортируем необходимые классы
import flash.geom.Rectangle;
import flash.geom.Point;
import flash.display.BitmapData;
// создаем два объекта прямоугольника, заданных точкой левого верхнего угла, а также шириной и высотой
var boundingBox_1 : Rectangle = new Rectangle (10,10, 200, 200);
var boundingBox_2 : Rectangle = new Rectangle (70,70, 200, 200);
// делаем проверки того:
//попадает ли точка с заданными координатами внутрь прямоугольника 1
trace ("point 1 in box = " +boundingBox_1.containsPoint(new Point (20, 30)));
// содержится ли целиком прямоугольник 2 внутри прямоугольника 1
trace ("box 1 contains box 2 = " +boundingBox_1.containsRectangle(boundingBox_2));
// пересекаются ли оба прямоугольника
trace ("box 1 intersects box 2 = " +boundingBox_1.intersects(boundingBox_2));
// функция, рисующая прямоугольник заданным цветом
function paintBox (num: Number, box: Rectangle, color : Number){
var mc:MovieClip = _root.createEmptyMovieClip("mc_" + num, this.getNextHighestDepth());
var bmp:BitmapData = new BitmapData(box.width, box.height, false, color);
mc.attachBitmap(bmp, mc.getNextHighestDepth());
mc._x = box.left;
mc._y = box.top;
mc._width = box.width;
mc._height = box.height;
}
// вызываем функцию рисования двух прямоугольников по очереди
paintBox (2, boundingBox_2, 0x0000FF00);
paintBox (1, boundingBox_1, 0x00FF0000);
//теперь нарисуем область пересечения двух прямоугольников
paintBox (3, boundingBox_2.intersection(boundingBox_1), 0x000000FF);
Алгоритм определения того, что происходит с объектами при соприкосновении, сильно зависит от природы этих объектов. Для упрощения рассмотрим ситуацию, когда на некоторую линию падает материальная точка. Заметьте: именно точка — не круг, не прямоугольник или иная фигура — пока только точка. В общем случае после падения происходит отскок объекта. Точка задается своей текущей координатой и указателем направления движения. Линия поверхности задается двумя точками (начальной и конечной). Две точки, точка и направление движения, — все это синонимы для понятия вектора. Нам необходимо определить, где происходит столкновение, а также вычислить вектор направления движения точки после этого. Сегодня мы разберем основы работы с векторами — сложные примеры требуют определенной подготовки, и я не хочу, чтобы вы набрали вслед за мной кусок кода, не понимая, что же там происходит. Итак, поехали. В простейшем случае вектор — это начальная точка и конечная. Их можно задать в actionscript, например, так (у меня все векторы — это объекты):
var vector = {start: {x: 10, y: 10}, end: {x: 20, y: 40}};
Зная начальную и конечную точки, вектор также можно определить как:
var vector = {start: {x: 10, y: 10}, delta: {x: 10, y: 30}}
здесь delta — это объект, хранящий внутри себя величины приращений, которые нужно добавить к начальной точке для того, чтобы вычислить конечную точку. Очевидно, что:
// вектор задается двумя точками: начальной и конечной
var vector = {start: {x: 10, y: 10}, end: {x: 20, y: 40}};
// вектор задается начальной точкой и величинами приращения — так, чтобы попасть в конечную точку
var vector2 = {start: {x: 10, y: 10}, delta: {x: 10, y: 30}}
// вычисляем компоненты вектора как разницу между конечной точкой и начальной
vector3 = {start: {x: vector.start.x, y: vector.start.y},
delta : {x: vector.end.x — vector.start.x, y: vector.end.y — vector.start.y} };
// векторы совпали
trace (vector3.delta.x == vector2.delta.x);
trace (vector3.delta.y == vector2.delta.y);
Для каждого вектора можно рассчитать его длину. Длина считается по формуле пифагоровых штанов, например, так:
vector3.len = Math.sqrt(vector3.delta.x*vector3.delta.x + vector3.delta.y*vector3.delta.y);
trace (vector3.len);
Также есть понятие нормализованного вектора, или вектора направления. Это такой вектор, длина которого равна единице. Вектор направления можно получить из обычного вектора путем деления величин приращения вектора на его длину.
var vector4 = {start: {x: vector3.start.x, x: vector3.start.x}, ort: {x: vector3.delta.x / vector3.len,y: vector3.delta.y / vector3.len}}; trace (vector4.ort.x + ", " + vector4.ort.y + " => "+ (vector4.ort.x*vector4.ort.x + vector4.ort.y*vector4.ort.y) );
В результате будет получено (как видите, длина такого вектора действительно равна точно единице):
0.316227766, 0.948683298 => 1
Векторы — классная штука, поскольку позволяют выполнять над собой сложные операции, не особенно задумываясь об углах. Ведь для решения об отскоке точки от стены мне достаточно было вспомнить правило, что угол падения равен углу отражения, правда, потом надо было бы вспоминать, как вычислить этот самый угол, и что он собой физически представляет именно в этой задаче моделирования отскока. На всякий случай привожу примеры, позволяющие преобразовывать вектора в углы, и наоборот. Считая, что delta.x и delta.y — это катеты треугольника с углом 90°, угол между этими катетами определяется как:
var angle_1=Math.atan2(vector3.delta.y, vector3.delta.x);
// не важно, между чем определять углы: величинами приращения начальной точки
var angle_2=Math.atan2(vector4.ort.y, vector4.ort.x);
// или составляющими нормализованного вектора
trace (angle_1 + " == " + angle_2);
// функция Math.atan2 возвращает величину угла именно в радианах — можно преобразовать ее в градусы
var angle_d =angle_1*180/Math.PI;
trace (angle_d);
// зная угол и длину вектора, можно вычислить величины его приращений
vector4.delta = {x : vector3.len * Math.cos (angle_1), y : vector3.len * Math.sin (angle_1)};
// смотрите: числа снова совпали — мы прошли путь от величин приращения к углам и назад
trace (vector4.delta.x +" == " + vector3.delta.x);
trace (vector4.delta.y +" == " + vector3.delta.y);
Почти последнее нужное нам понятие — нормаль к вектору. Вектор-нормаль — это такой вектор, который строго перпендикулярен нашему вектору — проще говоря, расположен под углом 90 градусов. Очевидно, что у каждого вектора есть целых два вектора-нормали — их называют правосторонние и левосторонние. Представьте, что, если вы стоите и смотрите, скажем, на окно, то вы вектор, который направлен в сторону окна. Теперь, если вы поднимете руки так, чтобы они образовали прямой угол с вашим телом, то слева будет левосторонний вектор-нормаль, а справа — очевидно, правосторонний.
// не забывайте, что в flash ось OY направлена сверху вниз
vector4.left = {delta: {x: — vector4.delta.y, y: vector4.delta.x}};
vector4.right = {delta: {x: vector4.delta.y, y: — vector4.delta.x}};
Теперь усложним ситуацию и введем второй вектор (в оригинальной задаче столкновения точки и стены ведь были два вектора, так что избежать еще одного математического ликбеза не удастся).
Первая операция — сложение двух векторов. Это очень простой случай. Например, если вы кидаете камень под углом 45 градусов, то на него действует сила вашего броска — это вектор №1, а также сила гравитации — это вектор №2. Реальная траектория полета будет чем-то промежуточным между этими двумя направлениями. Для получения результирующего вектора просто сложите соответствующие компоненты этих двух векторов, например, так: var vector5 ={delta: {x: vector2.delta.x + vector3.delta.x, y: vector2.delta.y + vector3.delta.y}};
Интересным является определение того, как два вектора ориентированы друг относительно друга, или какой между ними угол. Угол между двумя векторами определяется через их скалярное произведение.
// создаем еще один вектор
var vector6 = {ort: {x: Math.SQRT1_2, y: Math.SQRT1_2}, delta: {x: 10, y: 10}};
// вычислим длины участвующих в операции векторов
vector6.len = Math.sqrt(vector6.delta.x*vector6.delta.x + vector6.delta.y*vector6.delta.y);
vector4.len = Math.sqrt(vector4.delta.x*vector4.delta.x + vector4.delta.y*vector4.delta.y);
// и вычисляем угол между этими двумя векторами
var cos_alpha_1 = (vector4.delta.x*vector6.delta.x + vector4.delta.y*vector6.delta.y) / (vector4.len * vector6.len);
// если вычислять длину между нормализованными векторами, то не обязательно делить их на произведение длин
var cos_alpha_2 = (vector4.ort.x*vector6.ort.x + vector4.ort.y*vector6.ort.y);
trace (cos_alpha_1 + " == " + cos_alpha_2);
Теперь самое важное, что происходит при проецировании вектора vector4 на направление вектора vector6. Если нарисовать это на бумаге, то станет видно, что направление проекции совпадет с направлением вектора vector6. Будьте внимательны, когда проецируете: линия проекции должна быть перпендикулярна не оси OX, а именно самому вектору vector6.
var scalar_m = (vector4.delta.x*vector6.ort.x + vector4.delta.y*vector6.ort.y);
var vector_4_on_6 = {delta: {x: scalar_m * vector6.ort.x, y: scalar_m * vector6.ort.y }};
trace (vector_4_on_6.delta.x +", " + vector_4_on_6.delta.y);
Что же, сегодня мы неплохо поработали — фактически для решения задачи об отскоке точки от стены нам осталось только найти способ определить, где именно вектор точки пересечется с вектором стены. Затем мы сможем собрать все части головоломки вместе, ввести гравитацию, трение, потери энергии при отскоке и заставить все это работать вместе. При условии положительных откликов я также расскажу о моделировании поведения более сложных объектов. Также возможно ввести методы моделирования на основе verlet'ов, позволяющие запрограммировать практически что угодно при незначительных затратах процессорных ресурсов.
black zorro, black-zorro@tut.by
this.createTextField("status_txt", 999, 0, 0, 400, 22);
var mouseListener:Object = new Object();
mouseListener.onMouseMove = function():Void {
status_txt.text =
" layer0: " + _level0.hitTest(_xmouse, _ymouse, true) +
" object 1: " + _root.smb1_obj.hitTest(_xmouse, _ymouse, _root.chk_if_shape.selected) +
" object 2: " + _root.smb2_obj.hitTest(_xmouse, _ymouse, _root.chk_if_shape.selected) +
" object 3: " + _root.smb3_obj.hitTest(_xmouse, _ymouse, _root.chk_if_shape.selected)
;
}
Mouse.addListener(mouseListener);
smb_box_obj.onEnterFrame = function() {
_root.txt_status.text = this.hitTest(smb_circle_obj);
};
smb_circle_obj.onPress = function() {
this.startDrag(false);
updateAfterEvent();
};
smb_circle_obj.onRelease = function() {
this.stopDrag();
};
Результат работы виден на картинке 2. Обратите внимание на то, что надпись txt_status отмечает значение true (фигуры пересекаются) еще в тот момент, когда этого соприкосновения еще нет. На самом деле hitTest работает так: вокруг объектов рисуются ограничивающие их прямоугольники, и проверяется, не пересекаются ли сами фигуры, а именно: пересекаются ли ограничивающие их прямоугольники. Может быть, macromedia предусмотрела еще какие-то методы анализа. Увы, нет. Мы не можем не только точно определить, столкнулись ли два объекта, но и их дальнейшее поведение. Фактически если вы делаете игрушку, то создаете ее как набор жестко предопределенных сценариев поведения. Скажем, в гоночках, если машинка соприкоснулась с другой машинкой, она получает повреждения и отскакивает в сторону. Но является ли расчет количества повреждений и траектории отскока зависящим от того, как именно соприкоснулись эти два объекта? Были ли их траектории касательными, или же было лобовое столкновение? Боюсь, вам придется написать очень много проверок возможных ситуаций, если будете пользоваться подаренным macromedia методом hitTest. Так что придется нам, вооружившись отнятым у младшего брата или сестренки учебником по физике, реализовать пару алгоритмов самим. К счастью, задачи обнаружения пересечения объектов не только сложны, но и давно изучены.
Весь дальнейший материал ориентируется на 2d пространство. Методы работы с 3d во flash будут рассмотрены позже при условии появления откликов от читателей. Итак, процесс обнаружения того, соприкоснулись ли и как два объекта, начинается со стадии, когда определяется, какие пары объектов могут соприкоснуться (broad phase). Так, если у вас в сцене 100 объектов, то глупо перебивать все пары 100*100-1=9999 и запускать для каждой из них довольно трудоемкий алгоритм, определяющий конкретные детали такого соприкосновения. Для упрощенной проверки соприкосновения объектов мы создаем вокруг них bounding box (так же, как делает метод hitTest), а затем проверяем, пересекаются ли данные прямоугольники. Начиная с flash8 за это отвечает класс flash.geom.Rectangle. Если у вас фигура задается в общем случае некоторым полигоном, то вам нужно найти крайние точки: максимальные и минимальные координаты среди всех вершин полигона.
// импортируем необходимые классы
import flash.geom.Rectangle;
import flash.geom.Point;
import flash.display.BitmapData;
// создаем два объекта прямоугольника, заданных точкой левого верхнего угла, а также шириной и высотой
var boundingBox_1 : Rectangle = new Rectangle (10,10, 200, 200);
var boundingBox_2 : Rectangle = new Rectangle (70,70, 200, 200);
// делаем проверки того:
//попадает ли точка с заданными координатами внутрь прямоугольника 1
trace ("point 1 in box = " +boundingBox_1.containsPoint(new Point (20, 30)));
// содержится ли целиком прямоугольник 2 внутри прямоугольника 1
trace ("box 1 contains box 2 = " +boundingBox_1.containsRectangle(boundingBox_2));
// пересекаются ли оба прямоугольника
trace ("box 1 intersects box 2 = " +boundingBox_1.intersects(boundingBox_2));
// функция, рисующая прямоугольник заданным цветом
function paintBox (num: Number, box: Rectangle, color : Number){
var mc:MovieClip = _root.createEmptyMovieClip("mc_" + num, this.getNextHighestDepth());
var bmp:BitmapData = new BitmapData(box.width, box.height, false, color);
mc.attachBitmap(bmp, mc.getNextHighestDepth());
mc._x = box.left;
mc._y = box.top;
mc._width = box.width;
mc._height = box.height;
}
// вызываем функцию рисования двух прямоугольников по очереди
paintBox (2, boundingBox_2, 0x0000FF00);
paintBox (1, boundingBox_1, 0x00FF0000);
//теперь нарисуем область пересечения двух прямоугольников
paintBox (3, boundingBox_2.intersection(boundingBox_1), 0x000000FF);
Алгоритм определения того, что происходит с объектами при соприкосновении, сильно зависит от природы этих объектов. Для упрощения рассмотрим ситуацию, когда на некоторую линию падает материальная точка. Заметьте: именно точка — не круг, не прямоугольник или иная фигура — пока только точка. В общем случае после падения происходит отскок объекта. Точка задается своей текущей координатой и указателем направления движения. Линия поверхности задается двумя точками (начальной и конечной). Две точки, точка и направление движения, — все это синонимы для понятия вектора. Нам необходимо определить, где происходит столкновение, а также вычислить вектор направления движения точки после этого. Сегодня мы разберем основы работы с векторами — сложные примеры требуют определенной подготовки, и я не хочу, чтобы вы набрали вслед за мной кусок кода, не понимая, что же там происходит. Итак, поехали. В простейшем случае вектор — это начальная точка и конечная. Их можно задать в actionscript, например, так (у меня все векторы — это объекты):
var vector = {start: {x: 10, y: 10}, end: {x: 20, y: 40}};
Зная начальную и конечную точки, вектор также можно определить как:
var vector = {start: {x: 10, y: 10}, delta: {x: 10, y: 30}}
здесь delta — это объект, хранящий внутри себя величины приращений, которые нужно добавить к начальной точке для того, чтобы вычислить конечную точку. Очевидно, что:
// вектор задается двумя точками: начальной и конечной
var vector = {start: {x: 10, y: 10}, end: {x: 20, y: 40}};
// вектор задается начальной точкой и величинами приращения — так, чтобы попасть в конечную точку
var vector2 = {start: {x: 10, y: 10}, delta: {x: 10, y: 30}}
// вычисляем компоненты вектора как разницу между конечной точкой и начальной
vector3 = {start: {x: vector.start.x, y: vector.start.y},
delta : {x: vector.end.x — vector.start.x, y: vector.end.y — vector.start.y} };
// векторы совпали
trace (vector3.delta.x == vector2.delta.x);
trace (vector3.delta.y == vector2.delta.y);
Для каждого вектора можно рассчитать его длину. Длина считается по формуле пифагоровых штанов, например, так:
vector3.len = Math.sqrt(vector3.delta.x*vector3.delta.x + vector3.delta.y*vector3.delta.y);
trace (vector3.len);
Также есть понятие нормализованного вектора, или вектора направления. Это такой вектор, длина которого равна единице. Вектор направления можно получить из обычного вектора путем деления величин приращения вектора на его длину.
var vector4 = {start: {x: vector3.start.x, x: vector3.start.x}, ort: {x: vector3.delta.x / vector3.len,y: vector3.delta.y / vector3.len}}; trace (vector4.ort.x + ", " + vector4.ort.y + " => "+ (vector4.ort.x*vector4.ort.x + vector4.ort.y*vector4.ort.y) );
В результате будет получено (как видите, длина такого вектора действительно равна точно единице):
0.316227766, 0.948683298 => 1
Векторы — классная штука, поскольку позволяют выполнять над собой сложные операции, не особенно задумываясь об углах. Ведь для решения об отскоке точки от стены мне достаточно было вспомнить правило, что угол падения равен углу отражения, правда, потом надо было бы вспоминать, как вычислить этот самый угол, и что он собой физически представляет именно в этой задаче моделирования отскока. На всякий случай привожу примеры, позволяющие преобразовывать вектора в углы, и наоборот. Считая, что delta.x и delta.y — это катеты треугольника с углом 90°, угол между этими катетами определяется как:
var angle_1=Math.atan2(vector3.delta.y, vector3.delta.x);
// не важно, между чем определять углы: величинами приращения начальной точки
var angle_2=Math.atan2(vector4.ort.y, vector4.ort.x);
// или составляющими нормализованного вектора
trace (angle_1 + " == " + angle_2);
// функция Math.atan2 возвращает величину угла именно в радианах — можно преобразовать ее в градусы
var angle_d =angle_1*180/Math.PI;
trace (angle_d);
// зная угол и длину вектора, можно вычислить величины его приращений
vector4.delta = {x : vector3.len * Math.cos (angle_1), y : vector3.len * Math.sin (angle_1)};
// смотрите: числа снова совпали — мы прошли путь от величин приращения к углам и назад
trace (vector4.delta.x +" == " + vector3.delta.x);
trace (vector4.delta.y +" == " + vector3.delta.y);
Почти последнее нужное нам понятие — нормаль к вектору. Вектор-нормаль — это такой вектор, который строго перпендикулярен нашему вектору — проще говоря, расположен под углом 90 градусов. Очевидно, что у каждого вектора есть целых два вектора-нормали — их называют правосторонние и левосторонние. Представьте, что, если вы стоите и смотрите, скажем, на окно, то вы вектор, который направлен в сторону окна. Теперь, если вы поднимете руки так, чтобы они образовали прямой угол с вашим телом, то слева будет левосторонний вектор-нормаль, а справа — очевидно, правосторонний.
// не забывайте, что в flash ось OY направлена сверху вниз
vector4.left = {delta: {x: — vector4.delta.y, y: vector4.delta.x}};
vector4.right = {delta: {x: vector4.delta.y, y: — vector4.delta.x}};
Теперь усложним ситуацию и введем второй вектор (в оригинальной задаче столкновения точки и стены ведь были два вектора, так что избежать еще одного математического ликбеза не удастся).
Первая операция — сложение двух векторов. Это очень простой случай. Например, если вы кидаете камень под углом 45 градусов, то на него действует сила вашего броска — это вектор №1, а также сила гравитации — это вектор №2. Реальная траектория полета будет чем-то промежуточным между этими двумя направлениями. Для получения результирующего вектора просто сложите соответствующие компоненты этих двух векторов, например, так: var vector5 ={delta: {x: vector2.delta.x + vector3.delta.x, y: vector2.delta.y + vector3.delta.y}};
Интересным является определение того, как два вектора ориентированы друг относительно друга, или какой между ними угол. Угол между двумя векторами определяется через их скалярное произведение.
// создаем еще один вектор
var vector6 = {ort: {x: Math.SQRT1_2, y: Math.SQRT1_2}, delta: {x: 10, y: 10}};
// вычислим длины участвующих в операции векторов
vector6.len = Math.sqrt(vector6.delta.x*vector6.delta.x + vector6.delta.y*vector6.delta.y);
vector4.len = Math.sqrt(vector4.delta.x*vector4.delta.x + vector4.delta.y*vector4.delta.y);
// и вычисляем угол между этими двумя векторами
var cos_alpha_1 = (vector4.delta.x*vector6.delta.x + vector4.delta.y*vector6.delta.y) / (vector4.len * vector6.len);
// если вычислять длину между нормализованными векторами, то не обязательно делить их на произведение длин
var cos_alpha_2 = (vector4.ort.x*vector6.ort.x + vector4.ort.y*vector6.ort.y);
trace (cos_alpha_1 + " == " + cos_alpha_2);
Теперь самое важное, что происходит при проецировании вектора vector4 на направление вектора vector6. Если нарисовать это на бумаге, то станет видно, что направление проекции совпадет с направлением вектора vector6. Будьте внимательны, когда проецируете: линия проекции должна быть перпендикулярна не оси OX, а именно самому вектору vector6.
var scalar_m = (vector4.delta.x*vector6.ort.x + vector4.delta.y*vector6.ort.y);
var vector_4_on_6 = {delta: {x: scalar_m * vector6.ort.x, y: scalar_m * vector6.ort.y }};
trace (vector_4_on_6.delta.x +", " + vector_4_on_6.delta.y);
Что же, сегодня мы неплохо поработали — фактически для решения задачи об отскоке точки от стены нам осталось только найти способ определить, где именно вектор точки пересечется с вектором стены. Затем мы сможем собрать все части головоломки вместе, ввести гравитацию, трение, потери энергии при отскоке и заставить все это работать вместе. При условии положительных откликов я также расскажу о моделировании поведения более сложных объектов. Также возможно ввести методы моделирования на основе verlet'ов, позволяющие запрограммировать практически что угодно при незначительных затратах процессорных ресурсов.
black zorro, black-zorro@tut.by
Компьютерная газета. Статья была опубликована в номере 14 за 2007 год в рубрике программирование
