Steinberg WaveLab для самых начинающих
Я помню, как некогда "грыз гранит науки" в одном заведении — так там нас обучали компьютерам… в теории:). Да-да, вот именно то, что многие сейчас и подумали. То есть, мы чертили в конспектах Norton Commander:) и так далее. Конечно, поскольку у меня стоял тогда дома свой компьютер, все выглядело как мучение. Я не понимал сути происходящего процесса… Чтобы было более понятно: это все равно, что нарисовать на бумаге фортепианную клавиатуру и разучивать на ней фуги Баха, а потом сдавать по ним лабораторные на концертном рояле. В принципе, все так и выглядело. Именно поэтому у меня сейчас родилась идея не описывать программу по многочисленным просьбам читателей и не делать очередной вводный материал для начинающих, а совместить все в одном… Причем таким образом мы исключим множество лишних вопросов и, если нужно, заполним существующие пробелы.
Steinberg WaveLab… Звуковой редактор №1 в мире. Профессиональная энциклопедия в виде программы. Думается, этих эпитетов достаточно. Повествование будет о современном редактировании звука в целом, а WaveLab у нас выступит в качестве примера и опоры. Приступим…
Отображение звуковой волны. Основы номер 1
Как вы уже знаете, цифровой сигнал является выборкой определенных значений из непрерывного аналогового. А для тех, кто не знает, поясню. Человек воспринимает информацию, а она передается за счет сигнала. Сигнал проявляется в изменении какого-либо параметра — любого. В воздухе это изменения давления в среде, в электрическом токе — изменение напряжения и тока. Но мы воспринимаем все в непрерывном режиме, причем человека легко и обмануть. Вспомните кино с его 24-мя кадрами в секунду. Точно так же решили сделать и в звуке, то есть выяснили, с какой частотой нужно выбирать значения из непрерывного сигнала так, чтобы это не было заметно для человеческого уха. Это легло в теорию современного аудио, и как факт мы слушаем компакт-диски или МР3-файлы. Для того, чтобы объяснить, что происходит в устройстве аналого-цифрового преобразователя, можно и не мудрствовать особо. В каждый отсчет времени АЦП измеряет текущее напряжение в непрерывном аналоговом сигнале, сравнивает его с имеющейся шкалой своих напряжений и присваивает ближайшее подходящее. Таким образом, получается некая совокупность равномерно последовательно выбранных точек. В результате, открыв в WaveLab любой звуковой файл (меню File —> Open —> Wave), вы и увидите результаты действия АЦП, а для большей информативности можете рассмотреть волну при самом крупном масштабе.
Что вы увидите? Лесенку. Причем во многих других звуковых программах вместо нее точки выборки соединяются плавными линиями, но это неверно, поскольку между этими самыми точками никаких других значений и нет. Для эксперимента вы можете на панели курсоров мыши выбрать режим карандаша и попробовать нарисовать звуковую волну от руки, оставляя масштаб самым крупным. Что тогда произойдет? Редактор поведет себя как АЦП, то есть сделает выборку и присвоит свои ближайшие значения для точек, превращая нарисованную плавную линию в некое подобие лестницы. Количество выбранных значений за одну секунду называется частотой дискретизации (Sample Rate). Сам редактор WaveLab устроен таким образом, что при максимальном масштабе показывает посэмпловое (поточечное) разрешение при любых частотах дискретизации, но в теории, если бы вы нарисовали карандашом одну и ту же линию для файлов с различными значениями этой характеристики, количество "ступенек" в одном временном промежутке для каждого из случаев было бы различным. То есть, чем больше частота дискретизации, тем большим количеством выбранных значений вы оперируете. Но важно ли это? Вспомните пример с кино. Какая вам разница, 24 или 48 кадров будет воспроизводиться в секунду? И, в принципе, такое утверждение будет во многом верным, только вот в звуке есть один нюанс.
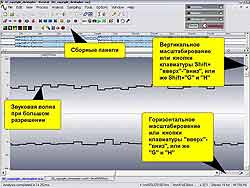Открываем программу, загружаем файл и рассматриваем его при большом масштабе
Помните, мы говорили, что АЦП сравнивает текущее значение непрерывного сигнала со своей шкалой значений? И что это за шкала такая? На самом деле это просто двоичный код с определенным количеством разрядов (или бит). То есть, существует некий диапазон, именуемый динамическим, который может описываться определенным количеством значений. Например, в двухбитном варианте их будет 2 во второй степени (то есть, 4), в трехбитном — 2 в третьей (т.е. 8) и т.д. Чем больше разрядность (битность, или Bitrate) преобразователя, тем больше точность его работы. И как раз эта цифровая характеристика является наиболее важной для описания качества цифрового звука. А частота дискретизации уже давно объяснена критериями Найквиста (теоремой Котельникова), и эту характеристику действительно нужно воспринимать, как и 24 кадра в кино (а в цифровом звуке распространен стандарт Красной Книги для аудио CD — 44,1 КГц). Именно поэтому во многих модулях обработки (плагинах) в качестве основного критерия указывается их разрядность, ведь в процессе работы появляется множество промежуточных значений, которые лучше учитывать, чем нет. Но при этом стоит отметить тот факт, что наилучшим вариантом является работа на повышенных и величине разрядности, и значении частоты дискретизации.
Отображение звуковой волны. Основы номер 2
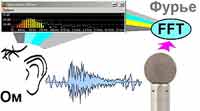
Открыв звуковой файл в обычном режиме, вы смотрите на звук только с одной, даже, можно сказать, однобокой, стороны, то есть вам показаны текущие изменения значений уровня сигнала в процессе времени (это называется амплитудно-временным представлением). Стоит отметить, что в природе звук таков и есть. Но наши органы слуха и мозг ведут себя как призма, то есть расщепляют сложную звуковую волну на ряд простых. Кстати, первым такое предположение сделал известный физик Георг Ом еще в 1820 году, а само преобразование такого характера было придумано чуть раньше Жаном-Батистом Жозефом Фурье. Для чего вам это нужно знать? Практически все звуковые программы современности позволяют графически показать внутреннее частотное наполнение звуковых файлов, кои по существу хранят в себе сложные волны. Причем по сравнению с XIX веком практически ничего не изменилось, разве что преобразования Фурье оптимизировали под цифровые вычислительные технологии. Для примера, запустите звуковой файл на воспроизведение и откройте индикатор FFT Meter (на панели горячих кнопок либо из меню Analysis —> Spectrum Analyser (FFT). В процессе воспроизведения вы наглядно увидите, как работает алгоритм Быстрого Преобразования Фурье (FFT — Fast Furie Transform).
FFT Meter и Spectrum Meter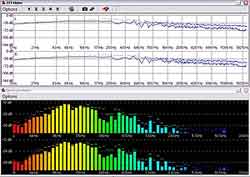
Если объяснять его суть простыми словами, то в каждый определенный момент из амплитудно-временного представления выбирается некоторое количество точек (фрагмент), из них формируется сложная периодическая функция, которая разбивается на ряд простых синусоидальных — получаем спектр. Длина этого фрагмента указывается заранее, и вы это можете увидеть, если зайдете в закладку Options —> Settings из окна данного индикатора. Оно (это количество) может быть как 512 точек, так и все 262.144 (максимально предусмотрено программой). Причем, если на тех же 512 точках вам будет казаться, что индикатор работает в режиме реального времени, то на 262.144 он будет менять изображение раз в три секунды на частоте дискретизации 44,1 КГц. Этот опыт вы можете проделать самостоятельно, а выводом из него будет являться то, что для Быстрого преобразования Фурье необходимо иметь определенное количество точек в амплитудно-временном представлении, чтобы потом построить представление частотное. А теперь посмотрите на другой схожий модуль, который в WaveLab называется Spectrum Meter (60 bands), а по существу является упрощенным вариантом FFT Meter. Структура преобразования сохранена практически та же, но при этом весь частотный спектр разбит на 60 полос. Точно такие же по сути, но менее профессиональные индикаторы вы можете увидеть в ряде пользовательских приложений — например, в WinAmp.
Отображение звуковой волны. Основы номер 3
Следующим этапом выделите некий фрагмент звукового файла и вызовите пункт меню Analysis —> 3D Frequency Analysis. Перед вами откроется трехмерный график с осями: время, амплитуда, частота. Именно это и есть правильное понимание и представление звука в целом. Таким его видят и звукорежиссеры, и программисты профессионального софта.
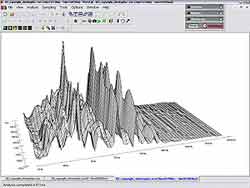Так выглядит 3D-график при условии, что амплитуда показана линейно
Давайте посмотрим на этот график более внимательно. На самом деле он построен очень умно. Например, если вы присмотритесь к нему в цветном исполнении (рисунки даны в черно-белом), то начиная от низких частот увидите "Каждый Охотник Знает Где Сидит Фазан" (в переводе со школьной поговорки для запоминания — Красный, Оранжевый, Зеленый, Голубой, Синий, Фиолетовый), то есть обозначено подобие нашего цветового и слухового восприятий. И на самом деле: зрение и слух у человека имеют очень много общего, а если говорить прямо, то и в видео, и в аудио часто используются одни и те же технологии и алгоритмы, только названы они по-разному. Кстати, не так давно был выпущен словарь, объясняющий звуковые термины для видеоспециалистов на их языке. Но это мы немного отстранились от темы. Возвращаемся. Часто у начинающих специалистов, особенно очень молодых, возникает простой и очевидный вопрос: а почему частотная шкала нелинейна, то есть на том же индикаторе FFT мы видим, что от 20 до 86 Гц занято столько же места, сколько и для диапазона от 2 до 14 КГц. Все дело в том, что так устроен наш слух. Данная шкала станет равномерной, если вы ее представите… хотя бы в виде фортепианной клавиатуры. А с физической точки зрения, то есть математическо-частотной, где измеряется количество колебаний в секунду, все выглядит неравномерно.
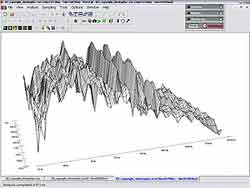Так выглядит 3D-график того же звукового фрагмента, но при условии, что амплитуда показана логарифмически
Точно так же и с амплитудным представлением звуковой волны (громкостью), ведь на самом деле децибельная шкала основана на десятичных логарифмах, и введена она неспроста, поскольку тоже описывает ощущения человека. Впрочем, вы в этом можете и сами убедиться, воспользовавшись тем, что в настройках данного 3D-графика можно произвести переключение частотной и амплитудной шкал в линейное либо логарифмическое представление. Это достаточно удобно с точки зрения информативности, а во-вторых — наглядно показывает разницу. В шестой версии WaveLab появилась новая возможность отображения звуковой волны в сонограммном виде.
Чтобы глубоко не лезть и не отходить от темы, отметим, что сонограмма представляет собой двухмерный вид нашего 3D-графика сверху, а по осям получается частота и время. Но параллельно с этим за счет специального цветового распределения показана амплитуда, то есть третья ось (амплитуда) существует неявно. Это очень удобно, причем в WaveLab такая возможность вывода информации появилась запоздало, поскольку до этого уже использовалась в ряде программ типа Adobe Audition. Благодаря такому представлению достаточно легко находить "всплески" на тех или иных частотах, что в обычном амплитудно-временном виде вычисляется достаточно трудно и, вообще-то, даже не видно.
Промежуточное завершение
В общем, любой гитарист вам может сказать, что начинать обучение лучше на дорогом инструменте, сделанном профессионалами. То же самое можно отнести и к звукорежиссуре.
Продолжение следует.
Кристофер, christopher@tut.by
Steinberg WaveLab… Звуковой редактор №1 в мире. Профессиональная энциклопедия в виде программы. Думается, этих эпитетов достаточно. Повествование будет о современном редактировании звука в целом, а WaveLab у нас выступит в качестве примера и опоры. Приступим…
Отображение звуковой волны. Основы номер 1
Как вы уже знаете, цифровой сигнал является выборкой определенных значений из непрерывного аналогового. А для тех, кто не знает, поясню. Человек воспринимает информацию, а она передается за счет сигнала. Сигнал проявляется в изменении какого-либо параметра — любого. В воздухе это изменения давления в среде, в электрическом токе — изменение напряжения и тока. Но мы воспринимаем все в непрерывном режиме, причем человека легко и обмануть. Вспомните кино с его 24-мя кадрами в секунду. Точно так же решили сделать и в звуке, то есть выяснили, с какой частотой нужно выбирать значения из непрерывного сигнала так, чтобы это не было заметно для человеческого уха. Это легло в теорию современного аудио, и как факт мы слушаем компакт-диски или МР3-файлы. Для того, чтобы объяснить, что происходит в устройстве аналого-цифрового преобразователя, можно и не мудрствовать особо. В каждый отсчет времени АЦП измеряет текущее напряжение в непрерывном аналоговом сигнале, сравнивает его с имеющейся шкалой своих напряжений и присваивает ближайшее подходящее. Таким образом, получается некая совокупность равномерно последовательно выбранных точек. В результате, открыв в WaveLab любой звуковой файл (меню File —> Open —> Wave), вы и увидите результаты действия АЦП, а для большей информативности можете рассмотреть волну при самом крупном масштабе.
Что вы увидите? Лесенку. Причем во многих других звуковых программах вместо нее точки выборки соединяются плавными линиями, но это неверно, поскольку между этими самыми точками никаких других значений и нет. Для эксперимента вы можете на панели курсоров мыши выбрать режим карандаша и попробовать нарисовать звуковую волну от руки, оставляя масштаб самым крупным. Что тогда произойдет? Редактор поведет себя как АЦП, то есть сделает выборку и присвоит свои ближайшие значения для точек, превращая нарисованную плавную линию в некое подобие лестницы. Количество выбранных значений за одну секунду называется частотой дискретизации (Sample Rate). Сам редактор WaveLab устроен таким образом, что при максимальном масштабе показывает посэмпловое (поточечное) разрешение при любых частотах дискретизации, но в теории, если бы вы нарисовали карандашом одну и ту же линию для файлов с различными значениями этой характеристики, количество "ступенек" в одном временном промежутке для каждого из случаев было бы различным. То есть, чем больше частота дискретизации, тем большим количеством выбранных значений вы оперируете. Но важно ли это? Вспомните пример с кино. Какая вам разница, 24 или 48 кадров будет воспроизводиться в секунду? И, в принципе, такое утверждение будет во многом верным, только вот в звуке есть один нюанс.
Помните, мы говорили, что АЦП сравнивает текущее значение непрерывного сигнала со своей шкалой значений? И что это за шкала такая? На самом деле это просто двоичный код с определенным количеством разрядов (или бит). То есть, существует некий диапазон, именуемый динамическим, который может описываться определенным количеством значений. Например, в двухбитном варианте их будет 2 во второй степени (то есть, 4), в трехбитном — 2 в третьей (т.е. 8) и т.д. Чем больше разрядность (битность, или Bitrate) преобразователя, тем больше точность его работы. И как раз эта цифровая характеристика является наиболее важной для описания качества цифрового звука. А частота дискретизации уже давно объяснена критериями Найквиста (теоремой Котельникова), и эту характеристику действительно нужно воспринимать, как и 24 кадра в кино (а в цифровом звуке распространен стандарт Красной Книги для аудио CD — 44,1 КГц). Именно поэтому во многих модулях обработки (плагинах) в качестве основного критерия указывается их разрядность, ведь в процессе работы появляется множество промежуточных значений, которые лучше учитывать, чем нет. Но при этом стоит отметить тот факт, что наилучшим вариантом является работа на повышенных и величине разрядности, и значении частоты дискретизации.
Отображение звуковой волны. Основы номер 2
Открыв звуковой файл в обычном режиме, вы смотрите на звук только с одной, даже, можно сказать, однобокой, стороны, то есть вам показаны текущие изменения значений уровня сигнала в процессе времени (это называется амплитудно-временным представлением). Стоит отметить, что в природе звук таков и есть. Но наши органы слуха и мозг ведут себя как призма, то есть расщепляют сложную звуковую волну на ряд простых. Кстати, первым такое предположение сделал известный физик Георг Ом еще в 1820 году, а само преобразование такого характера было придумано чуть раньше Жаном-Батистом Жозефом Фурье. Для чего вам это нужно знать? Практически все звуковые программы современности позволяют графически показать внутреннее частотное наполнение звуковых файлов, кои по существу хранят в себе сложные волны. Причем по сравнению с XIX веком практически ничего не изменилось, разве что преобразования Фурье оптимизировали под цифровые вычислительные технологии. Для примера, запустите звуковой файл на воспроизведение и откройте индикатор FFT Meter (на панели горячих кнопок либо из меню Analysis —> Spectrum Analyser (FFT). В процессе воспроизведения вы наглядно увидите, как работает алгоритм Быстрого Преобразования Фурье (FFT — Fast Furie Transform).
FFT Meter и Spectrum Meter
Если объяснять его суть простыми словами, то в каждый определенный момент из амплитудно-временного представления выбирается некоторое количество точек (фрагмент), из них формируется сложная периодическая функция, которая разбивается на ряд простых синусоидальных — получаем спектр. Длина этого фрагмента указывается заранее, и вы это можете увидеть, если зайдете в закладку Options —> Settings из окна данного индикатора. Оно (это количество) может быть как 512 точек, так и все 262.144 (максимально предусмотрено программой). Причем, если на тех же 512 точках вам будет казаться, что индикатор работает в режиме реального времени, то на 262.144 он будет менять изображение раз в три секунды на частоте дискретизации 44,1 КГц. Этот опыт вы можете проделать самостоятельно, а выводом из него будет являться то, что для Быстрого преобразования Фурье необходимо иметь определенное количество точек в амплитудно-временном представлении, чтобы потом построить представление частотное. А теперь посмотрите на другой схожий модуль, который в WaveLab называется Spectrum Meter (60 bands), а по существу является упрощенным вариантом FFT Meter. Структура преобразования сохранена практически та же, но при этом весь частотный спектр разбит на 60 полос. Точно такие же по сути, но менее профессиональные индикаторы вы можете увидеть в ряде пользовательских приложений — например, в WinAmp.
Отображение звуковой волны. Основы номер 3
Следующим этапом выделите некий фрагмент звукового файла и вызовите пункт меню Analysis —> 3D Frequency Analysis. Перед вами откроется трехмерный график с осями: время, амплитуда, частота. Именно это и есть правильное понимание и представление звука в целом. Таким его видят и звукорежиссеры, и программисты профессионального софта.
Давайте посмотрим на этот график более внимательно. На самом деле он построен очень умно. Например, если вы присмотритесь к нему в цветном исполнении (рисунки даны в черно-белом), то начиная от низких частот увидите "Каждый Охотник Знает Где Сидит Фазан" (в переводе со школьной поговорки для запоминания — Красный, Оранжевый, Зеленый, Голубой, Синий, Фиолетовый), то есть обозначено подобие нашего цветового и слухового восприятий. И на самом деле: зрение и слух у человека имеют очень много общего, а если говорить прямо, то и в видео, и в аудио часто используются одни и те же технологии и алгоритмы, только названы они по-разному. Кстати, не так давно был выпущен словарь, объясняющий звуковые термины для видеоспециалистов на их языке. Но это мы немного отстранились от темы. Возвращаемся. Часто у начинающих специалистов, особенно очень молодых, возникает простой и очевидный вопрос: а почему частотная шкала нелинейна, то есть на том же индикаторе FFT мы видим, что от 20 до 86 Гц занято столько же места, сколько и для диапазона от 2 до 14 КГц. Все дело в том, что так устроен наш слух. Данная шкала станет равномерной, если вы ее представите… хотя бы в виде фортепианной клавиатуры. А с физической точки зрения, то есть математическо-частотной, где измеряется количество колебаний в секунду, все выглядит неравномерно.
Точно так же и с амплитудным представлением звуковой волны (громкостью), ведь на самом деле децибельная шкала основана на десятичных логарифмах, и введена она неспроста, поскольку тоже описывает ощущения человека. Впрочем, вы в этом можете и сами убедиться, воспользовавшись тем, что в настройках данного 3D-графика можно произвести переключение частотной и амплитудной шкал в линейное либо логарифмическое представление. Это достаточно удобно с точки зрения информативности, а во-вторых — наглядно показывает разницу. В шестой версии WaveLab появилась новая возможность отображения звуковой волны в сонограммном виде.
Промежуточное завершение
В общем, любой гитарист вам может сказать, что начинать обучение лучше на дорогом инструменте, сделанном профессионалами. То же самое можно отнести и к звукорежиссуре.
Продолжение следует.
Кристофер, christopher@tut.by
Компьютерная газета. Статья была опубликована в номере 32 за 2006 год в рубрике мультимедиа
