О двусвязном списке и операциях над ним
О двусвязном списке и операциях над ним
— Вы не подскажете, как мне выбраться отсюда?
— Это смотря куда ты хочешь добраться.
— Да мне уж все равно…
— Тогда все равно, куда идти.
Л. Кэрролл, "Алиса в стране Чудес"
В процессе программирования задачи, ориентированной на обработку сколь-нибудь большого количества данных, рано или поздно встает вопрос о том, как же хранение этих данных реализовать. Современные системы программирования: Visual C++, Delphi или C++ Builder, — предоставляют в распоряжение разработчика многочисленные типы данных, позволяющие эффективно распределять память и выполнять различные операции над хранимыми данными. Они детально спроектированы добросовестными сотрудниками Microsoft и Borland/Inprise, прошли жесткое тестирование и успешно используются в многочисленных проектах. Однако если вы цените компактность кода, не отягощенного массивными динамическими библиотеками, и используете нетрадиционные, однако свободно распространяемые среды, например, "Ассемблер", то у вас под рукой может и не оказаться подходящего набора подпрограмм. В этом случае остается надеяться только на свои силы и вспомнить то, что читалось на лекциях по программированию.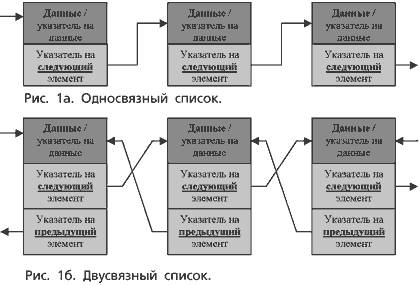
Речь в этой статье пойдет о двусвязном списке и методах работы с ним. Это понятие, несомненно, знакомо большинству студентов технических вузов и многим школьникам, увлеченным информатикой в том смысле, в котором ее понимал классик этого предмета академик А.П. Ершов. Динамические структуры данных, как следует из их названия, предназначены для хранения записей, количество которых заранее неизвестно и может изменяться в процессе выполнения программы. Основным достоинством хранения информации в динамических структурах является то их свойство, что память расходуется только по мере необходимости, в отличие от статических массивов. Существенным недостатком является сложность понимания их работы и в конечном счете сложность алгоритмов, реализующих действия над ними.
По опыту знакомства с учебной литературой можно отметить одну закономерность. Как правило, тему динамических структур данных открывает односвязный список — структура, в которой каждый элемент знает, какой элемент следующий (рис. 1а). После разъяснения на наглядных примерах способов добавления элементов в список и удаления из него отмечают неудобство использования односвязных списков ввиду единственно возможного направления их просмотра. Если вы "проскочили" нужный элемент, найти предыдущий можно только повторив перебор всех элементов начиная с первого, на который, как правило, заводится указатель Head. Естественным способом решения описанной проблемы является добавление к каждому элементу списка указателя на предыдущий элемент, осуществляя таким образом переход к двусвязному списку (рис. 1б). Хотя уже сам факт ввода "двусторонних" указателей качественно изменяет исходную структуру, для симметрии обычно добавляют указатель Tail на последний элемент списка.
И если для односвязного списка алгоритмы операций выглядели достаточно лаконично, то такое, на первый взгляд, незначительное изменение структуры вводит в эти алгоритмы дополнительные ветвления, что, с одной стороны, затрудняет их понимание, а с другой снижает эффективность реализации. Кроме того, увеличение потенциальных возможностей новой структуры данных приводит к экстенсивному расширению операций над ней. Например, поиск элемента от начала или конца списка реализуется различными процедурами (или в одной процедуре есть альтернатива с двумя симметричными ветвями).
Основная причина этих трудностей видится в стремлении разработчиков четко указать, где у списка "начало", а где "конец", и в соответствии с этим обозначить направление движения по списку. Это стремление прослеживается в именовании соответствующих идентификаторов Head/Tail (голова/хвост) и Next/Prev (следующий/предыдущий).
С другой стороны, всем известна поговорка о палке о двух концах. В этой фразе заключается инвариантность двух сторон этого деревянного цилиндра. Почему бы не взглянуть на двусвязный список с этой точки зрения? Тогда для хранения указателей на крайние элементы списка можно использовать массив из двух указателей. Следуя традиции в обозначениях, опишем его так:
Head: array [0..1] of address;
Аналогичным образом опишем массив Next указателей на соседние элементы, который будем использовать вместо отдельных указателей Next/Prev в записи об элементе списка:
item = record
data: address; // указатель на данные;
next: array [0..1] of address; // указатели на соседей
end;
Внимательные читатели, вероятно, уже заметили некоторую вольность в стиле приведенных описаний. Дело в том, что автор решил использовать подмножество языка Modula-2, реализованное в среде "Странник Модула-Си-Паскаль" А.Ю. Андреева. Она позиционируется как бесплатная система разработки приложений для Windows, ее описание и обсуждение заслуживает отдельной статьи, а познакомиться с ней можно на страничке http:// home.perm.ru/~strannik. Надеюсь, что всем, кто знаком с Паскалем (языком программирования, конечно, а не знаменитым французским ученым), такое описание будет понятным, да и приверженцы других языков тоже разберутся.
Продолжая анализ предлагаемого способа организации двусвязного списка, заметим, что как выбор "головы" списка, так и выбор направления его просмотра определяется значением индекса соответствующего массива. Причем раз направлений всего два, удобно ввести операцию, которая по заданному направлению может определить обратное. Опишем ее в виде процедуры Reverse следующим образом:
procedure Reverse (i: byte): byte;
begin
return (i+1) mod 2
end;
Очевидно, эта функция инвертирует значение i по принципу логической операции NOT. Она очень пригодится при разработке алгоритмов работы с двусвязным списком, к которой как раз пришло время приступить.
Для примера автор предлагает реализовать операции вставки элемента в произвольную позицию списка, удаления произвольного элемента из списка и поиска элемента в списке по его порядковому номеру. Приступая к описанию, нужно предупредить читателя, что, возможно, набор алгоритмов, предложенных его вниманию, покажется неполным, а, быть может, и не совсем корректным. С другой стороны, он способен удовлетворить многие практические нужды разработчика, а главное — продемонстрировать изящество работы со списком.
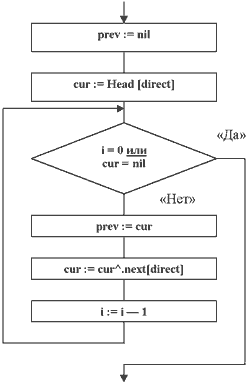
Рис. 2а. Алгоритм поиска позиции в списке по ее номеру i.
Итак, за дело. Но нужно не забыть выполнить инициализацию нового списка, которая заключается в присвоении всем элементам массива Head значений nil (элементы в списке отсутствуют). После инициализации кажется логичным начать добавлять элементы в список. Однако для этого нужно найти позицию вставки нового элемента. Удобно описать эту позицию через указатели на два соседних элемента, предыдущий и текущий, которые образуют "вилку" и между которыми будет вставлен новый элемент. Введем два вспомогательных указателя: cur — на текущий элемент, prev — на элемент предыдущий. Остальное расскажет блок-схема, изображенная на рис. 2а. Параметр direct, принимающий значение "0" или "1", указывает направление просмотра списка: "от головы" или "с хвоста"; i определяет искомую позицию: 0 — перед первым элементом, 1 — между первым и вторым — и т.д. Если в списке элементов меньше, чем (i + 1), то новый элемент будет добавлен после последнего (с учетом выбранного направления direct). Таким образом, получилась универсальная процедура, позволяющая просматривать список в любом направлении. Обратите внимание и на тот факт, что она не содержит альтернатив — для ее реализации хватило одного цикла "пока".
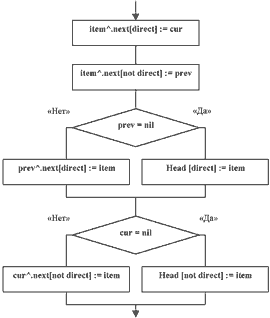
Рис. 2б. Алгоритм вставки элемента item между элементами prev и cur.
После того, как позиция найдена, элемент можно добавить. Добавить означает разорвать связь между элементами cur и prev и увязать их со вставляемым элементом. Как это происходит, расскажет блок-схема на рис. 2б. Вопрос выбора указателя на следующий или предыдущий элемент относительно текущего решается очень просто с помощью параметра, указывающего направление, и введенной ранее операции Reverse (кстати, в блок-схеме с целью экономии места она заменена операцией not).
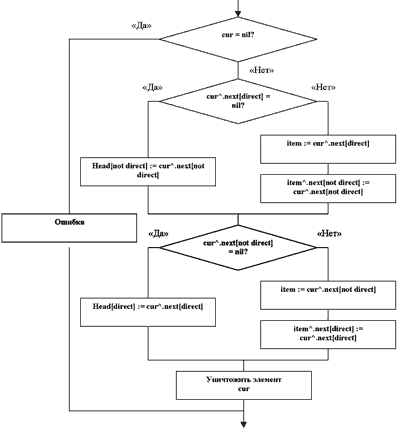
Рис. 2в. Алгоритм удаления элемента cur из списка.
Чтобы выполнить удаление элемента, воспользуемся алгоритмом, который проиллюстрирован блок-схемой рис. 2в. Поиск удаляемого элемента должен быть осуществлен уже рассмотренной выше процедурой поиска, только параметр i в этом случае будет иметь следующий смысл: 0 — удалить первый элемент, 1 — удалить второй элемент и т.д. Если элементов меньше, чем значение (i + 1), удаление выполняться не будет.
Рассмотренные способы работы с двусвязным списком могут служить базой для разработки других операций, например, последовательного обхода списка. Однако приведенные алгоритмы хорошо выполняют основную задачу, которую ставил перед собой автор, — продемонстрировать инвариантность направления просмотра двусвязного списка и упростить с учетом этого свойства алгоритмы работы с ним. Симметрия приведенных блок-схем и отсутствие лишних алгоритмических конструкций наглядно подтверждают все то, о чем было сказано в статье.
Игорь Орещенков, 2004 г.
компьютерная газета
— Вы не подскажете, как мне выбраться отсюда?
— Это смотря куда ты хочешь добраться.
— Да мне уж все равно…
— Тогда все равно, куда идти.
Л. Кэрролл, "Алиса в стране Чудес"
В процессе программирования задачи, ориентированной на обработку сколь-нибудь большого количества данных, рано или поздно встает вопрос о том, как же хранение этих данных реализовать. Современные системы программирования: Visual C++, Delphi или C++ Builder, — предоставляют в распоряжение разработчика многочисленные типы данных, позволяющие эффективно распределять память и выполнять различные операции над хранимыми данными. Они детально спроектированы добросовестными сотрудниками Microsoft и Borland/Inprise, прошли жесткое тестирование и успешно используются в многочисленных проектах. Однако если вы цените компактность кода, не отягощенного массивными динамическими библиотеками, и используете нетрадиционные, однако свободно распространяемые среды, например, "Ассемблер", то у вас под рукой может и не оказаться подходящего набора подпрограмм. В этом случае остается надеяться только на свои силы и вспомнить то, что читалось на лекциях по программированию.

Речь в этой статье пойдет о двусвязном списке и методах работы с ним. Это понятие, несомненно, знакомо большинству студентов технических вузов и многим школьникам, увлеченным информатикой в том смысле, в котором ее понимал классик этого предмета академик А.П. Ершов. Динамические структуры данных, как следует из их названия, предназначены для хранения записей, количество которых заранее неизвестно и может изменяться в процессе выполнения программы. Основным достоинством хранения информации в динамических структурах является то их свойство, что память расходуется только по мере необходимости, в отличие от статических массивов. Существенным недостатком является сложность понимания их работы и в конечном счете сложность алгоритмов, реализующих действия над ними.
По опыту знакомства с учебной литературой можно отметить одну закономерность. Как правило, тему динамических структур данных открывает односвязный список — структура, в которой каждый элемент знает, какой элемент следующий (рис. 1а). После разъяснения на наглядных примерах способов добавления элементов в список и удаления из него отмечают неудобство использования односвязных списков ввиду единственно возможного направления их просмотра. Если вы "проскочили" нужный элемент, найти предыдущий можно только повторив перебор всех элементов начиная с первого, на который, как правило, заводится указатель Head. Естественным способом решения описанной проблемы является добавление к каждому элементу списка указателя на предыдущий элемент, осуществляя таким образом переход к двусвязному списку (рис. 1б). Хотя уже сам факт ввода "двусторонних" указателей качественно изменяет исходную структуру, для симметрии обычно добавляют указатель Tail на последний элемент списка.
И если для односвязного списка алгоритмы операций выглядели достаточно лаконично, то такое, на первый взгляд, незначительное изменение структуры вводит в эти алгоритмы дополнительные ветвления, что, с одной стороны, затрудняет их понимание, а с другой снижает эффективность реализации. Кроме того, увеличение потенциальных возможностей новой структуры данных приводит к экстенсивному расширению операций над ней. Например, поиск элемента от начала или конца списка реализуется различными процедурами (или в одной процедуре есть альтернатива с двумя симметричными ветвями).
Основная причина этих трудностей видится в стремлении разработчиков четко указать, где у списка "начало", а где "конец", и в соответствии с этим обозначить направление движения по списку. Это стремление прослеживается в именовании соответствующих идентификаторов Head/Tail (голова/хвост) и Next/Prev (следующий/предыдущий).
С другой стороны, всем известна поговорка о палке о двух концах. В этой фразе заключается инвариантность двух сторон этого деревянного цилиндра. Почему бы не взглянуть на двусвязный список с этой точки зрения? Тогда для хранения указателей на крайние элементы списка можно использовать массив из двух указателей. Следуя традиции в обозначениях, опишем его так:
Head: array [0..1] of address;
Аналогичным образом опишем массив Next указателей на соседние элементы, который будем использовать вместо отдельных указателей Next/Prev в записи об элементе списка:
item = record
data: address; // указатель на данные;
next: array [0..1] of address; // указатели на соседей
end;
Внимательные читатели, вероятно, уже заметили некоторую вольность в стиле приведенных описаний. Дело в том, что автор решил использовать подмножество языка Modula-2, реализованное в среде "Странник Модула-Си-Паскаль" А.Ю. Андреева. Она позиционируется как бесплатная система разработки приложений для Windows, ее описание и обсуждение заслуживает отдельной статьи, а познакомиться с ней можно на страничке http:// home.perm.ru/~strannik. Надеюсь, что всем, кто знаком с Паскалем (языком программирования, конечно, а не знаменитым французским ученым), такое описание будет понятным, да и приверженцы других языков тоже разберутся.
Продолжая анализ предлагаемого способа организации двусвязного списка, заметим, что как выбор "головы" списка, так и выбор направления его просмотра определяется значением индекса соответствующего массива. Причем раз направлений всего два, удобно ввести операцию, которая по заданному направлению может определить обратное. Опишем ее в виде процедуры Reverse следующим образом:
procedure Reverse (i: byte): byte;
begin
return (i+1) mod 2
end;
Очевидно, эта функция инвертирует значение i по принципу логической операции NOT. Она очень пригодится при разработке алгоритмов работы с двусвязным списком, к которой как раз пришло время приступить.
Для примера автор предлагает реализовать операции вставки элемента в произвольную позицию списка, удаления произвольного элемента из списка и поиска элемента в списке по его порядковому номеру. Приступая к описанию, нужно предупредить читателя, что, возможно, набор алгоритмов, предложенных его вниманию, покажется неполным, а, быть может, и не совсем корректным. С другой стороны, он способен удовлетворить многие практические нужды разработчика, а главное — продемонстрировать изящество работы со списком.

Рис. 2а. Алгоритм поиска позиции в списке по ее номеру i.
Итак, за дело. Но нужно не забыть выполнить инициализацию нового списка, которая заключается в присвоении всем элементам массива Head значений nil (элементы в списке отсутствуют). После инициализации кажется логичным начать добавлять элементы в список. Однако для этого нужно найти позицию вставки нового элемента. Удобно описать эту позицию через указатели на два соседних элемента, предыдущий и текущий, которые образуют "вилку" и между которыми будет вставлен новый элемент. Введем два вспомогательных указателя: cur — на текущий элемент, prev — на элемент предыдущий. Остальное расскажет блок-схема, изображенная на рис. 2а. Параметр direct, принимающий значение "0" или "1", указывает направление просмотра списка: "от головы" или "с хвоста"; i определяет искомую позицию: 0 — перед первым элементом, 1 — между первым и вторым — и т.д. Если в списке элементов меньше, чем (i + 1), то новый элемент будет добавлен после последнего (с учетом выбранного направления direct). Таким образом, получилась универсальная процедура, позволяющая просматривать список в любом направлении. Обратите внимание и на тот факт, что она не содержит альтернатив — для ее реализации хватило одного цикла "пока".

Рис. 2б. Алгоритм вставки элемента item между элементами prev и cur.
После того, как позиция найдена, элемент можно добавить. Добавить означает разорвать связь между элементами cur и prev и увязать их со вставляемым элементом. Как это происходит, расскажет блок-схема на рис. 2б. Вопрос выбора указателя на следующий или предыдущий элемент относительно текущего решается очень просто с помощью параметра, указывающего направление, и введенной ранее операции Reverse (кстати, в блок-схеме с целью экономии места она заменена операцией not).

Рис. 2в. Алгоритм удаления элемента cur из списка.
Чтобы выполнить удаление элемента, воспользуемся алгоритмом, который проиллюстрирован блок-схемой рис. 2в. Поиск удаляемого элемента должен быть осуществлен уже рассмотренной выше процедурой поиска, только параметр i в этом случае будет иметь следующий смысл: 0 — удалить первый элемент, 1 — удалить второй элемент и т.д. Если элементов меньше, чем значение (i + 1), удаление выполняться не будет.
Рассмотренные способы работы с двусвязным списком могут служить базой для разработки других операций, например, последовательного обхода списка. Однако приведенные алгоритмы хорошо выполняют основную задачу, которую ставил перед собой автор, — продемонстрировать инвариантность направления просмотра двусвязного списка и упростить с учетом этого свойства алгоритмы работы с ним. Симметрия приведенных блок-схем и отсутствие лишних алгоритмических конструкций наглядно подтверждают все то, о чем было сказано в статье.
Игорь Орещенков, 2004 г.
компьютерная газета
Компьютерная газета. Статья была опубликована в номере 39 за 2004 год в рубрике программирование :: разное


