Обучение, самоорганизация и эволюция как методы в искусственном интеллекте
Обучение, самоорганизация и эволюция как методы в искусственном интеллекте
Нейронные сети. Самообучение и самоорганизация.
Самоорганизация — термин более широкий, поскольку включает в себя не только самообучение (изменение значений весов), но и возможности изменения структуры связей, количества нейронов.
Самообучение — в данном случае обучение без учителя, когда сеть сама учится классифицировать подаваемые ей образы без внешней оценки.
Такие сети применяют для решения задач распознавания образов, оптимизации, управления, сжатия данных.
Коснемся самообучения по методу Хебба и конкурентного самообучения сетей Кохонена. Прямое распространение информации в таких сетях аналогично рассмотренному.
По методу Хебба усиливаются связи между возбужденными нейронами [2]:
сигнальный метод обучения Хебба:
,
дифференциальный метод обучения Хебба:
.
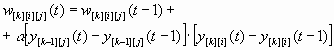Цикл подачи обучающих образов продолжается до тех пор, пока выходные значения сети не стабилизируются с заданной точностью. Такая сеть способна обобщать одинаковые образы, относя их к одному классу. Для представления результатов обучения сети в удобной форме сеть можно дополнить одним слоем и обучить этот слой по методу обратного распространения ошибки.
В сетях Кохонена применяется конкурентное обучение — изменяются веса только одного нейрона (победителя), выходное значение которого было максимально для данного слоя [9]. Для адекватной подстройки весов входные значения и веса необходимо постоянно поддерживать в нормализованном виде, подстройка весов выглядит так:
.
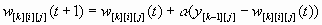Чтобы избежать ситуации, когда некоторые нейроны могут оказаться исключенными из процесса обучения вообще, можно изменять веса непобедивших нейронов с намного меньшим шагом или вести статистику побед, уменьшая возможности победы для слишком частых победителей [9].
После обучения в процессе функционирования сети Кохонена активируется только один победивший нейрон, выходы всех остальных — нулевые.
Какие преимущества дает самоорганизация ИНС [4]:
Применение принципов самоорганизации позволяет синтезировать многослойные нейронные сети минимальной конфигурации на неполной, непредставительной обучающей выборке.
Для синтеза нейронной сети, обеспечивающей минимальное число ошибок на обучающей выборке, не требуется заранее оценивать значимость входных переменных (признаков), задавать число слоев и нейронов в них, а также определять синаптические связи. Конфигурация обученной нейронной сети будет минимальной.
Минимальная конфигурация необходима по двум причинам:
Нейронная сеть оптимальной сложности обладает наибольшей обобщающей (и следовательно прогностической) способностью. Такую нейронную сеть трудно переобучить.
Решающие правила, реализуемые нейронной сетью оптимальной сложности, существенно легче интерпретировать, если представить их в символьной форме логических выражений, понятных пользователю.
Такие сети также предоставляют механизм извлечения трудноформализуемых знаний. Обучив сеть на примерах из некоторой трудноформализуемой области и получив минимальную конфигурацию сети, можно затем синтезировать формальное представление знаний, приобретенных сетью.
Генетический алгоритм. Эволюция и поиск.
Генетический алгоритм (ГА), позаимствованный у природных аналогов, является наиболее ярким представителем эволюционных методов и представляет собой мощнейшее поисковое средство [2,7,10,11,12], имеющее важное значение при решении различных проблем. Поскольку качество решения обычно оценивается некоторой оценочной функцией, ГА также называют методом оптимизации многоэкстремальных функций. Никакой дополнительной информации о решаемой задаче ГА больше не имеет. Решение, получаемое при помощи ГА, по своему характеру субоптимально, но это не мешает применять ГА для поиска глобальных экстремумов. В процессе эволюции популяция вырабатывает качества, необходимые для выживания и приспособления, и которые одновременно и являются оптимальным решением. ГА отлично себя зарекомендовали на NP-трудных задачах (рис. 6), например таких, как задача коммивояжера. В [11] указывается такая характеристика оценки пригодности ГА, как минимизация количества вычислений целевой функции.
рис. 6
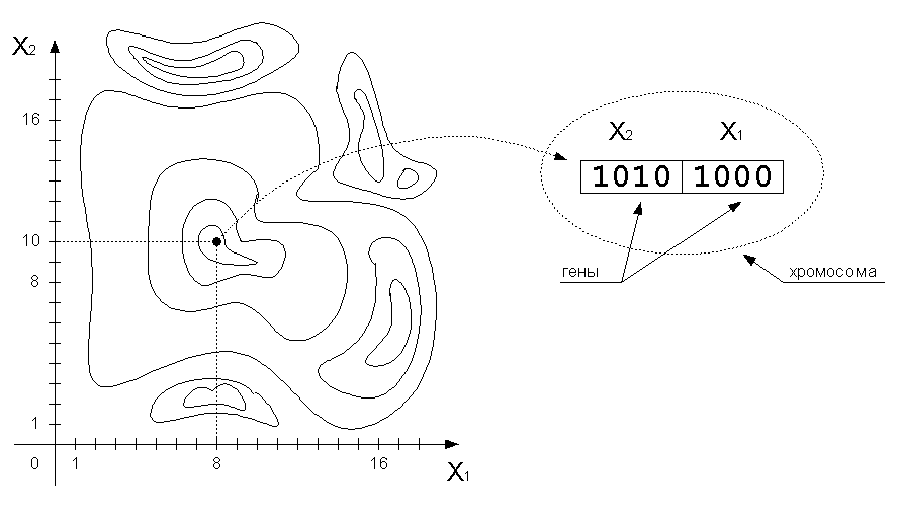
рис. 7
Таблица 1.
В общем виде генетический алгоритм таков [2,7,10]:
Задается функция оптимальности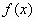
, определяющая эффективность каждого найденного решения, для отслеживания выхода решения из допустимой области в функцию можно включить штрафной компонент. Каждое решение кодируется как вектор x, называемый хромосомой. Его элементы — гены, изменяющиеся в определенных позициях, называемых аллелями (рис. 7). Обычно хромосомы представляются в двоичном целочисленном виде или двоичном с плавающей запятой. В некоторых случаях более эффективно будет использование кода Грея (табл. 1), в котором изменение одного бита в любой позиции приводит к изменению значения на единицу. Для некоторых задач двоичное представление естественно, для других задач может оказаться полезным отказаться от двоичного представления. В общем случае выбор способа представления параметров задачи в виде хромосомы влияет на эффективность решения. Популяция — совокупность решений на конкретной итерации, количество хромосом в популяции 
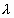задается изначально и в процессе обычно не изменяется. Для ГА пока не существует таких же четких математических основ, как для НС, поэтому при реализации ГА возможны различные вариации.
Оператор отбора. Служит для создания промежуточной популяции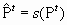
. В промежуточную популяцию копируются хромосомы из текущей популяции в соответствии с их вероятностью воспроизведения P i . Существуют различные схемы отбора, самая популярная из них — пропорциональный отбор: 
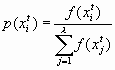. Для устранения зависимости от положительных значений и влияний больших чисел используется масштабирование оценок или ранжирование [10]. Пропорциональный отбор не гарантирует сохранности лучших результатов, достигнутых в какой-либо популяции, и для преодоления такого явления используется элитный отбор, который всегда сохраняет наилучшую хромосому.
Воспроизведение. Служит для создания следующей популяции на основе промежуточной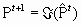
при помощи операторов кроссинговера и мутации, которые имеют случайный характер. Каждому элементу промежуточной популяции 
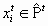, если надо, подбирается партнер, и вновь созданная хромосома помещается в новую популяцию.
Оператор кроссинговера. Производит обмен генетического материала между родителями для получения потомков. Простейший одноточечный кроссинговер (рис. 8) производит обмен частями, на которые хромосома разбивается точкой кроссинговера, выбираемой случайно. Двухточечный кроссинговер обменивает кусок строки, попавшей между двумя точками. Предельным случаем является равномерный кроссинговер, в результате которого все биты хромосом обмениваются с некоторой вероятностью. Этот оператор служит для исследования новых областей пространства и улучшения существующих (приспособление).
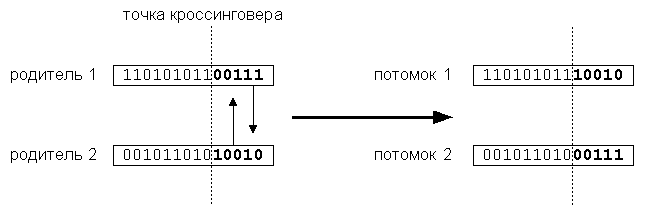
рис. 8
Оператор мутации. К каждому биту хромосомы с небольшой вероятностью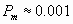
применяется мутация — т.е. бит (аллель) изменяет значение на противоположный (рис. 9). Мутация нужна для расширения пространства поиска (исследование) и предотвращения невосстановимой потери бит в аллелях.
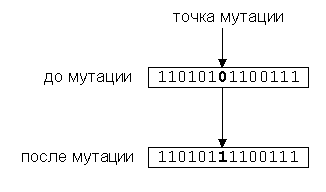
рис. 9
Существует также оператор воспроизведения, называемый инверсией, который заключается в реверсировании бит между двумя случайными позициями, однако для большинства задач он не имеет практического смысла и поэтому неэффективен [10].
Важно понять, почему ГА вообще работоспособен и почему он настолько эффективен. Во-первых, различные параметры в реальных системах в большинстве своем слабосвязаны [2], т.е. постепенное изменение одного из них не требует радикального изменения второго для восстановления оптимальности (рис. 7), что позволяет исследовать пространство. Во-вторых, функции оптимальности все-таки имеют спуски и подъемы и не являются сплошным изрезанным полем, что создает почву для постепенного приспособления.
Для исследования эффективности ГА используем понятие шаблона [7,10,11,12]. Шаблон определяется с помощью элементов множества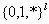
, где l — длина хромосомы в битах, * — в данной позиции может быть любой бит (рис. 10). Шаблоны — это гиперплоскости различной размерности в l — мерном пространстве. Порядок 
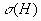шаблона определяется количеством зафиксированных позиций (которые равны 0 или 1). Длина 
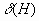шаблона — расстояние между первой и последней зафиксированной позицией. На самом деле ГА обрабатывает не строки, а шаблоны, и может производить выборку значительного числа гиперплоскостей из областей с высокой приспособленностью. В течение одного поколения популяции оценивается 
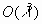структур, хотя популяция содержит только 
индивидуумов. Этот эффект называется неявный параллелизм. На практике же это означает, что увеличение числа особей популяции экспоненциально ускоряет решение задачи [11]. Это и отличает ГА от различных эвристических и случайно-поисковых методов, в которых единственное решение развивается само по себе, а начав заново, не помнит предыдущего опыта.
Существует теорема Холланда о шаблонах, из которой следует, что короткие (по отношению к кроссинговеру), низкого порядка (по отношению к мутации) и имеющие оптимальность выше средней шаблоны увеличивают свое представительство в последовательности поколений экспоненциально. Такой шаблон называется строительным блоком.
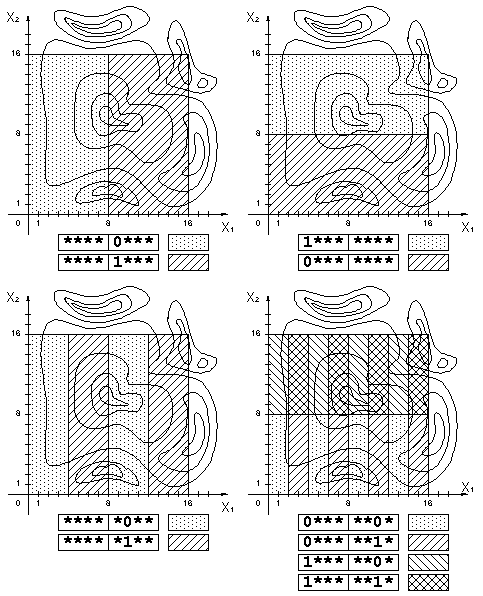
рис. 10
Отметим наиболее актуальные проблемы ГА и интересные модификации ГА.
Неудачный выбор упорядочивания и кодирования битов в хромосоме может вызвать преждевременное схождение к локальному оптимуму, ведя алгоритм по ложному пути [10]. Для преодоления этого недостатка можно выбирать способ кодирования, основываясь на дополнительной информации о задаче. Существуют также мобильные ГА, с переменной длиной хромосом. Для некоторых задач такое представление естественно, для других надо вводить специальные правила чтения хромосом. Вместо оператора кроссинговера используются оператор разрезания строк (CUT), вероятность которого повышается с увеличением длины строки, и оператор сцепления строк (SPLICE), который выбирает из популяции два куска и сцепляет их в один кусок. Популяция представляет собой совокупность пере- и недоопределенных строк. Правила чтения таких строк могут быть, например, такими: в переопределенной строке при чтении слева направо не учитываются уже использованные гены, а в недоопределенных строках отсутствующие места заимствуются у лучшего элемента.
Проблема баланса исследования новых областей и приспособления к найденным [12]. Это необходимо для предотвращения преждевременной сходимости к локальному оптимуму. В [12] используются модифицированные способы отбора хромосом в промежуточную популяцию (отказ от вероятностных принципов в пользу элитного и отбора с вытеснением) и выбора родительской пары (случайный, селективный, на основе близкого или дальнего родства).
Влияние длины хромосомы на преждевременную сходимость. В [11,12] используется символьная модель для разбиения пространства поиска на диапазоны с целью уменьшения длины хромосомы.
Интересные результаты может дать сочетание ГА с другими методами [7,10].
Заключение
Кроме приведенных методов, существуют и другие, используемые для различных задач, связанных с обучением, самоорганизацией, поиском. Хотелось бы еще отметить наличие такого мощного метода, как метод группового учета аргументов — МГУА (Group Method of Data Handling, GMDH), который тоже относится к разряду эволюционных [2,13], и голографическую нейросетевую парадигму [3], привлекающую более глубокие принципы функционирования мозга.
Приведенные методы являются частью целого среди методов такого класса и иллюстрируют неотъемлемые принципы создания систем нового поколения. В науке происходит накопление критической информации, которое в ближайшее время должно привести к переходу на качественно иной уровень, ведущий к следующей ступени развития искусственных информационных систем [6].
Литература
P.S.
Оригинал этой (и предыдущей) статьи, а также простенький пример к методу обратного распространения можно скачать на http://bdv78.newmail.ru Интересующие вас вопросы, связанные с искусственным интеллектом, можно задать на AI-Forum'е: http://www.pool-7.ru/alexkuck/aiforum. Автор выражает огромную благодарность Сергею Балтаку за неоценимую информационную поддержку. Если будут пожелания — возможно дальнейшее развитие этой темы, в частности обзор других видов нейросетей, доступное объяснение основных принципов их функционирования, применение нейросетей на практике; другие методы искусственного интеллекта.
Дмитрий Брилюк
bdv78@newmail.ru
http://bdv78.newmail.ru
(c) компьютерная газета
Нейронные сети. Самообучение и самоорганизация.
Самоорганизация — термин более широкий, поскольку включает в себя не только самообучение (изменение значений весов), но и возможности изменения структуры связей, количества нейронов.
Самообучение — в данном случае обучение без учителя, когда сеть сама учится классифицировать подаваемые ей образы без внешней оценки.
Такие сети применяют для решения задач распознавания образов, оптимизации, управления, сжатия данных.
Коснемся самообучения по методу Хебба и конкурентного самообучения сетей Кохонена. Прямое распространение информации в таких сетях аналогично рассмотренному.
По методу Хебба усиливаются связи между возбужденными нейронами [2]:
сигнальный метод обучения Хебба:
дифференциальный метод обучения Хебба:
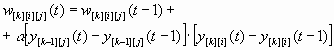
Цикл подачи обучающих образов продолжается до тех пор, пока выходные значения сети не стабилизируются с заданной точностью. Такая сеть способна обобщать одинаковые образы, относя их к одному классу. Для представления результатов обучения сети в удобной форме сеть можно дополнить одним слоем и обучить этот слой по методу обратного распространения ошибки.
В сетях Кохонена применяется конкурентное обучение — изменяются веса только одного нейрона (победителя), выходное значение которого было максимально для данного слоя [9]. Для адекватной подстройки весов входные значения и веса необходимо постоянно поддерживать в нормализованном виде, подстройка весов выглядит так:
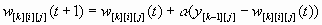
Чтобы избежать ситуации, когда некоторые нейроны могут оказаться исключенными из процесса обучения вообще, можно изменять веса непобедивших нейронов с намного меньшим шагом или вести статистику побед, уменьшая возможности победы для слишком частых победителей [9].
После обучения в процессе функционирования сети Кохонена активируется только один победивший нейрон, выходы всех остальных — нулевые.
Какие преимущества дает самоорганизация ИНС [4]:
Применение принципов самоорганизации позволяет синтезировать многослойные нейронные сети минимальной конфигурации на неполной, непредставительной обучающей выборке.
Для синтеза нейронной сети, обеспечивающей минимальное число ошибок на обучающей выборке, не требуется заранее оценивать значимость входных переменных (признаков), задавать число слоев и нейронов в них, а также определять синаптические связи. Конфигурация обученной нейронной сети будет минимальной.
Минимальная конфигурация необходима по двум причинам:
Нейронная сеть оптимальной сложности обладает наибольшей обобщающей (и следовательно прогностической) способностью. Такую нейронную сеть трудно переобучить.
Решающие правила, реализуемые нейронной сетью оптимальной сложности, существенно легче интерпретировать, если представить их в символьной форме логических выражений, понятных пользователю.
Такие сети также предоставляют механизм извлечения трудноформализуемых знаний. Обучив сеть на примерах из некоторой трудноформализуемой области и получив минимальную конфигурацию сети, можно затем синтезировать формальное представление знаний, приобретенных сетью.
Генетический алгоритм. Эволюция и поиск.
Генетический алгоритм (ГА), позаимствованный у природных аналогов, является наиболее ярким представителем эволюционных методов и представляет собой мощнейшее поисковое средство [2,7,10,11,12], имеющее важное значение при решении различных проблем. Поскольку качество решения обычно оценивается некоторой оценочной функцией, ГА также называют методом оптимизации многоэкстремальных функций. Никакой дополнительной информации о решаемой задаче ГА больше не имеет. Решение, получаемое при помощи ГА, по своему характеру субоптимально, но это не мешает применять ГА для поиска глобальных экстремумов. В процессе эволюции популяция вырабатывает качества, необходимые для выживания и приспособления, и которые одновременно и являются оптимальным решением. ГА отлично себя зарекомендовали на NP-трудных задачах (рис. 6), например таких, как задача коммивояжера. В [11] указывается такая характеристика оценки пригодности ГА, как минимизация количества вычислений целевой функции.
рис. 6
рис. 7
Таблица 1.
Целое | Двоичный код | Код Грея |
0 | 0000 | 0000 |
1 | 0001 | 0001 |
2 | 0010 | 0011 |
3 | 0011 | 0010 |
4 | 0100 | 0110 |
5 | 0101 | 0111 |
6 | 0110 | 0101 |
7 | 0111 | 0100 |
8 | 1000 | 1100 |
9 | 1001 | 1101 |
10 | 1010 | 1111 |
11 | 1011 | 1110 |
12 | 1100 | 1010 |
13 | 1101 | 1011 |
14 | 1110 | 1001 |
15 | 1111 | 1000 |
В общем виде генетический алгоритм таков [2,7,10]:
Задается функция оптимальности
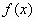
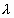
Начальная популяцияможет быть инициализирована как случайными значениями, так и некоторыми готовыми решениями.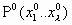
Каждая хромосома популяции x i оценивается функцией эффективности, и ей в соответствии с этой оценкой присваивается вероятность воспроизведения P i .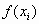
В соответствии с вероятностями воспроизведения P i генерируется новая популяция хромосом, причем с большей вероятностью воспроизводятся наиболее эффективные элементы. Воспроизведение осуществляется при помощи генетических операторов кроссинговера (скрещивание) и мутации.
Если найдено удовлетворительное решение, процесс останавливается, иначе продолжается с шага 2.
Оператор отбора. Служит для создания промежуточной популяции
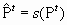
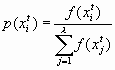
Воспроизведение. Служит для создания следующей популяции на основе промежуточной
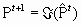
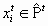
Оператор кроссинговера. Производит обмен генетического материала между родителями для получения потомков. Простейший одноточечный кроссинговер (рис. 8) производит обмен частями, на которые хромосома разбивается точкой кроссинговера, выбираемой случайно. Двухточечный кроссинговер обменивает кусок строки, попавшей между двумя точками. Предельным случаем является равномерный кроссинговер, в результате которого все биты хромосом обмениваются с некоторой вероятностью. Этот оператор служит для исследования новых областей пространства и улучшения существующих (приспособление).
рис. 8
Оператор мутации. К каждому биту хромосомы с небольшой вероятностью
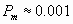
рис. 9
Существует также оператор воспроизведения, называемый инверсией, который заключается в реверсировании бит между двумя случайными позициями, однако для большинства задач он не имеет практического смысла и поэтому неэффективен [10].
Важно понять, почему ГА вообще работоспособен и почему он настолько эффективен. Во-первых, различные параметры в реальных системах в большинстве своем слабосвязаны [2], т.е. постепенное изменение одного из них не требует радикального изменения второго для восстановления оптимальности (рис. 7), что позволяет исследовать пространство. Во-вторых, функции оптимальности все-таки имеют спуски и подъемы и не являются сплошным изрезанным полем, что создает почву для постепенного приспособления.
Для исследования эффективности ГА используем понятие шаблона [7,10,11,12]. Шаблон определяется с помощью элементов множества
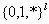
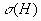
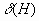
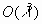
Существует теорема Холланда о шаблонах, из которой следует, что короткие (по отношению к кроссинговеру), низкого порядка (по отношению к мутации) и имеющие оптимальность выше средней шаблоны увеличивают свое представительство в последовательности поколений экспоненциально. Такой шаблон называется строительным блоком.
рис. 10
Отметим наиболее актуальные проблемы ГА и интересные модификации ГА.
Неудачный выбор упорядочивания и кодирования битов в хромосоме может вызвать преждевременное схождение к локальному оптимуму, ведя алгоритм по ложному пути [10]. Для преодоления этого недостатка можно выбирать способ кодирования, основываясь на дополнительной информации о задаче. Существуют также мобильные ГА, с переменной длиной хромосом. Для некоторых задач такое представление естественно, для других надо вводить специальные правила чтения хромосом. Вместо оператора кроссинговера используются оператор разрезания строк (CUT), вероятность которого повышается с увеличением длины строки, и оператор сцепления строк (SPLICE), который выбирает из популяции два куска и сцепляет их в один кусок. Популяция представляет собой совокупность пере- и недоопределенных строк. Правила чтения таких строк могут быть, например, такими: в переопределенной строке при чтении слева направо не учитываются уже использованные гены, а в недоопределенных строках отсутствующие места заимствуются у лучшего элемента.
Проблема баланса исследования новых областей и приспособления к найденным [12]. Это необходимо для предотвращения преждевременной сходимости к локальному оптимуму. В [12] используются модифицированные способы отбора хромосом в промежуточную популяцию (отказ от вероятностных принципов в пользу элитного и отбора с вытеснением) и выбора родительской пары (случайный, селективный, на основе близкого или дальнего родства).
Влияние длины хромосомы на преждевременную сходимость. В [11,12] используется символьная модель для разбиения пространства поиска на диапазоны с целью уменьшения длины хромосомы.
Интересные результаты может дать сочетание ГА с другими методами [7,10].
Заключение
Кроме приведенных методов, существуют и другие, используемые для различных задач, связанных с обучением, самоорганизацией, поиском. Хотелось бы еще отметить наличие такого мощного метода, как метод группового учета аргументов — МГУА (Group Method of Data Handling, GMDH), который тоже относится к разряду эволюционных [2,13], и голографическую нейросетевую парадигму [3], привлекающую более глубокие принципы функционирования мозга.
Приведенные методы являются частью целого среди методов такого класса и иллюстрируют неотъемлемые принципы создания систем нового поколения. В науке происходит накопление критической информации, которое в ближайшее время должно привести к переходу на качественно иной уровень, ведущий к следующей ступени развития искусственных информационных систем [6].
Литература
Информатика. Энциклопедический словарь для начинающих / Под ред. Д.А. Поспелова — М: Педагогика-Пресс, 1994, — 350 с.
Курс лекций по предмету "Основы проектирования систем с искусственным интеллектом" / Сост. Сотник С.Л. —URL: http://www.neuropower.de
Кузнецов О.П. О некомпьютерных подходах к моделированию интеллектуальных процессов мозга — Москва, Институт проблем управления РАН
Самоорганизующиеся нейронные сети и их применение — URL: http://www.chat.ru/~neurolab
Редько В.Г. Курс лекций "Эволюционная кибернетика" — URL: http://inet.keldysh.ru/BioCyber/Lectures.html
Головко В.А. Нейроинтеллект: Теория и применения Книга 1 Организация и обучение нейронных сетей с прямыми и обратными связями — Брест: БПИ, 1999, — 260 с.
E-Mail: cm@brpi.belpak.brest.by
Змитрович А. И. Интеллектуальные информационные системы — Минск: Тетрасистемс, 1997, — 368 с.
Лосик Г.В. Сенсомоторная теория персептрона — E-Mail: losik@newman.bas-net.ru
Головко В.А. Нейроинтеллект: Теория и применения Книга 2 Самоорганизация, отказоустойчивость и применение нейронных сетей — Брест: БПИ, 1999, — 228 с.E-Mail: cm@brpi.belpak.brest.by
Скурихин А.Н. Генетические алгоритмы / Новости искусственного интеллекта, 1995, №4, с. 6-46.
С.А. Исаев. Генетические алгоритмы — эволюционные методы поиска URL: http://rv.ryazan.ru/~bug/library/ai/isaev/2/part1.html
Д.И. Батищев, С.А. Исаев Оптимизация многоэкстремальных функций с помощью генетических алгоритмов URL: http://bspu.secna.ru/Docs/~saisa/ga/summer97.html
Group Method of Data Handling URL: http://www.inf.kiev.ua/GMDH-home
P.S.
Оригинал этой (и предыдущей) статьи, а также простенький пример к методу обратного распространения можно скачать на http://bdv78.newmail.ru Интересующие вас вопросы, связанные с искусственным интеллектом, можно задать на AI-Forum'е: http://www.pool-7.ru/alexkuck/aiforum. Автор выражает огромную благодарность Сергею Балтаку за неоценимую информационную поддержку. Если будут пожелания — возможно дальнейшее развитие этой темы, в частности обзор других видов нейросетей, доступное объяснение основных принципов их функционирования, применение нейросетей на практике; другие методы искусственного интеллекта.
Дмитрий Брилюк
bdv78@newmail.ru
http://bdv78.newmail.ru
(c) компьютерная газета
Компьютерная газета. Статья была опубликована в номере 47 за 2000 год в рубрике разное :: мелочи жизни
