Статьи из номера 2000/26
Радиоприемник принимает Интернет-станции
2000/26‣del :: новости

НОВОСТИ КОМПЬЮТЕРНАЯ ГАЗЕТА КОМПЬЮТЕРНАЯ ХРОНИКА Радиоприемник принимает Интернет-станции Первый выпущенный фирмой Thomson Интернет-радиоприемник будет продаваться в США под маркой RCA и использовать службу Kerbango Tuning Service. Тюнер AM/FM/IM (Internet Modulation) подключается к Интернет через Ethernet-порт настольного компьютера, что позволяет получить доступ к тысячам развлекательных каналов. Ориентированный первоначально на ... подробнее
Вышел очередной номер газеты. В номере:
2000/26
Вышел очередной номер газеты. В номере: — в рубрике "расставим точки над i": структурированные кабельные системы -— информационно-аналитический материал и описания наиболее популярных продуктов различных производителей — репортаж с выставки "Связь-Экспокомм'2000", проходившей в середине мая в Москве; — краткий обзор утилит удаленного администрирования; — совет специалиста: простой и эффективный способ подключения к Интернет на основе решений ... подробнее
The Sims выйдет и на Mac'ах
2000/26‣виртуальные радости :: Новости из мира игр
Новости из мира игр The Sims выйдет и на Mac'ах Новость для любителей Macintosh. Компания Westlake Interactive объявила о том, что перевод хита от компании Maxis и EA под названием The Sims на платформу Macintosh достиг стадии бета-тестирования. Подробнее об этом можно узнать на сайте www.aspyr.com . Steel Panthers исправляется Компания Matrix Games в прошлом месяце представила свой новый продукт под названием Steel Panthers World At War ... подробнее
В ближайшие несколько месяцев в офисах Управления картографии США в ряде штатов появятся электронные киоски, позволяющие получить топографическую карту любого места на территории США. Заказчик сможет
2000/26‣del :: А знаете ли вы, что...?
А знаете ли вы, что...? • В ближайшие несколько месяцев в офисах Управления картографии США в ряде штатов появятся электронные киоски, позволяющие получить топографическую карту любого места на территории США. Заказчик сможет ввести координаты или названия населенных пунктов, а компьютер по базе данных Управления попытается найти соответствующую информацию. Затем при помощи программ Wildflower Productions Topo! и TrailSmart будет сгенерирована ... подробнее
Через пять лет их будет 270 миллионов
2000/26‣del :: Прогнозы, анализ, статистика
Прогнозы, анализ и статистика Через пять лет их будет 270 миллионов В недавнем отчете компании Datamonitor говорится, что к 2005 году уже 270 млн. европейцев получат доступ к услугам мобильной телефонии. Около 69% владельцев мобильных телефонов будут использовать для подключения к Internet службы, основанные на протоколе WAP. Рост числа абонентов мобильной телефонии в Европе обусловлен, прежде всего, наступлением мобильных ... подробнее
Станислав Лем. Информационные встряски
2000/26‣del :: del
Станислав Лем. Информационные встряски Как уже известно всем читателям газет в мире, федеральное правительство США вместе с толпой прокуроров, представляющих отдельные штаты, начало процесс против Microsoft, тем самым против Билла Гейтса, обвиняемого в противоречащих законодательству США попытках монополизации сетевого рынка, а точнее, в вытеснении с этого рынка интернетовских просмотровых программ (браузеров) других фирм. Так как обе ... подробнее
CD-RW привод BTC BCE432IE
2000/26‣hard :: приводы

CD-RW привод BTC BCE432IE В последнее время, когда видео и аудио в цифре постепенно вытесняют древний способ записи на магнитную пленку, cd-rw приводы становятся очень актуальным приобретением. Что касается видео, то с появлением формата divx или mpeg4 полнометражный фильм с приличным качеством изображения и великолепным звуком занимает приблизительно 500-600 Мб, что как раз умещается на диск. Если говорить об аудио, то тут тоже есть ряд ... подробнее
Лишь о 3D мечтая... Часть II. Продолжение
2000/26‣hard :: video

Лишь о 3D мечтая... Часть II. Продолжение G400 g-400 - процессор нового поколения для 1999. Прежде всего g400 выделяется использованием новой технологии наложения объемных текстур (enviroment bump maping). Эффект смотрится потрясающе красиво и реализован во многих новых играх. Но обо всем по порядку. Производится этот чип по технологическому процессу 0.25мкм. Частоты работы чипа - 125 МГц, памяти - 166 МГц. RAMDAC 300 МГц. Максимальное ... подробнее
Photoshop 5.5. Первые шаги 1
2000/26‣soft :: графика
Photoshop 5.5. Первые шаги Перед тем как начать свою статью, я хотел бы выразить благодарность всем читателям, которые писали мне, отзываясь на публикации прошлых моих статей. Большое спасибо. Пользуясь случаем, хочу извиниться за то, что не смог ответить, так как свой старый модем продал, а до покупки нового руки не доходят - сессия все силы и желания убивает как наповал;). Надеюсь, организационный вопрос уладили. Теперь перейдем ... подробнее
Шпионим и создаем презентации одновременно
2000/26‣soft :: системные программы
Шпионим и создаем презентации одновременно Однажды, когда я в очередной раз наводил порядок на своем жестком диске, я обнаружил необычную утилитку. Предыстория сей утилиты такова. Блуждая ночью по различным сайтам, я наткнулся на программу, которая мне жутко понравилась. На протяжении нескольких недель я использовал скачанную мной программу в разных целях. Вы скажете, что такого не бывает, чтобы одна и та же программа, да по-разному ... подробнее
Фейерверк web-дизайна, или Кое-что о Fireworks
2000/26‣soft :: интернет
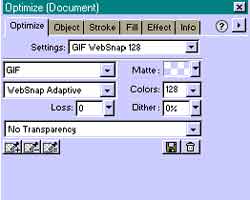
Фейерверк web-дизайна, или Кое-что о fireworks Иногда мне кажется, что жизнь обходит меня стороной. В самый последний момент я узнаю, что, оказывается, есть некое тайное общество влиятельных лиц, решающих судьбу белорусского Интернета. Они собираются в одном из минских ресторанов для обсуждения насущных байнетовских проблем. Они решают, чему быть, а чему пригрозить указательным пальцем. Страшно подумать, вдруг и ты попадешь под их рачительный ... подробнее
Биплан это стильно...
2000/26‣виртуальные радости :: нет данных

Биплан это стильно... Игра: hunt for the red baron. Разработчик/Издатель: fiendish games. Жанр: Аркадный симулятор биплана. Системные требования: p2-233/32 mb ram/3d accelerator И вновь развеселая компания разработчиков Fiendish Games беспокоится, чтобы мы не скучали от безделья за своим рабочим компом. Немногим ранее она выпустила в свет передовой трехмерный Columns под названием Towers of Ancients, который отличался потрясной графикой, ... подробнее
daikatana
2000/26‣виртуальные радости :: нет данных
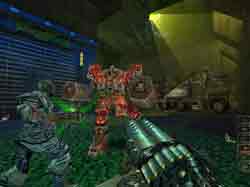
daikatana Наконец-то компакт-диск долгожданной DAIKATANA появился на прилавках магазинов и торговых точек. Честно говоря, я уже думал, что мы будем ждать сие творение незабвенного Джона Ромеро так же долго, как и Duke Nukem Forever (долгострой на ту же action-тему). Но не единожды откладываемый проект все же увидел свет. И что мы имеем? Было ли ради чего так долго ждать? Давайте разберемся. Самое главное в новой игре от великого и ужасного ... подробнее
StarLancer
2000/26‣виртуальные радости :: нет данных

starlancer microsoft предлагает нам управлять не многочисленными воинами с топорами и другими большими ножиками, а космическим истребителем. По жанру новая игра - это экшен-симулятор. Место действия: ближний космос, солнечная система. Время действия: ближайшее. Сохранились некоторые великие Земные державы, но Земля и, соответственно, подконтрольное жителям нашего зелено-голубого шарика околосолнечное космическое пространство разделено между ... подробнее
MDK 2
2000/26‣виртуальные радости :: нет данных

mdk 2 Не одна неделя и даже не один месяц... Да что там! Не один год прошел с того времени, как свет увидел революционный, для того уровня игровых технологий, проект - MDK. Именно в этой игре мы впервые смогли увидеть настоящую снайперскую винтовку и воспользоваться ею самым серьезным образом, кроме того, именно в MDK мы познакомились с по-настоящему трехмерными персонажами и, тогда еще слабыми, возможностями первых ускорителей трехмерной ... подробнее
Официальный тест MCSE 70-068: Windows NT 4.0 Server Enterprise.
2000/26‣литература :: разное

ОБЗОР ЛИТЕРАТУРЫ Перкович Д. Официальный тест MCSE 70-068: Windows NT 4.0 Server Enterprise. Пер. с англ. — М.: Издательско-торговый дом "Русская Редакция", 1999. — 400 с.; ил. Эта книга представляет собой официальное пособие для подготовки к ключевому экзамену в программе сертификации специалистов по операционной системе Microsoft Windows NT. Читатель получит полное представление о том, какие именно знания и практические навыки проверяются ... подробнее


