Статьи из номера 2000/11
Новая рабочая станция от Acer
2000/11‣del :: новости

Новая рабочая станция от Acer Acer CIS Inc. представила настольный компьютер Veriton FP как флагмана новой линейки рабочих станций компании Acer. Это концептуально новая модель, созданная для профессионалов, которые ценят дизайн и эргономичность рабочего места. В то же время Veriton FP — мощная рабочая станция, построенная на базе процессоров Intel Pentium III. Она поставляется с 128 мегабайтами оперативной памяти типа SDRAM ECC и ... подробнее
Новый номер сетевых решений уже в продаже! Еще лучше и еще толще! ;)
2000/11‣del :: del
Intel приобрела датскую фирму GIGA A/S Корпорация Intel объявила, что пришла к окончательному соглашению о приобретении входящей в группу NKT компании GIGA A/S со штаб-квартирой в Копенгагене (Дания). Сумма сделки оценивается приблизительно в 1.25 млрд долларов США. C 1997 года, когда Intel приобрела Case Technology A/S, в Дании работает техническое представительство корпорации. В 1999 году она также привлекла к работе персонал Olicom A/S. ... подробнее
Техники из компаний Xerox и Sharp демонстрируют "интеллектуальную" систему подачи чернил, которую обе фирмы намерены применить в нов
2000/11‣del :: новости
С Hewlett-Packard легче бороться вместе Техники из компаний Xerox и Sharp демонстрируют "интеллектуальную" систему подачи чернил, которую обе фирмы намерены применить в новых недорогих струйных принтерах, предназначенных для домашнего и офисного использования. Отдельные емкости для краски каждого цвета позволят заменять только опустевший картридж, а не все вместе, избегая лишних затрат, характерных для однокартриджных систем, ... подробнее
Сотрудничество ради будущего
2000/11‣del :: беларусь

Четырнадцатого марта фирма ASBIS Enterprises проводила для своих ключевых партнеров специализированный семинар, посвященный обзору и рекламе новых продуктов мирового компьютерного гиганта IBM и недавно купленной этой корпорацией компании Mylex. Непосредственно речь шла о накопителях на жестких дисках, которыми IBM славилась всегда, и о новых RAID-контроллерах от Mylex, одного из ведущих производителей в этой области компьютерной техники. ... подробнее
Думаю, что многих, как и меня, волнует вопрос о выгорании люминесцентного слоя монитора. Года 3 назад приобрел 14' монитор фирмы Samsung. До сегодняш
2000/11‣разное :: тусовка
Думаю, что многих, как и меня, волнует вопрос о выгорании люминесцентного слоя монитора. Года 3 назад приобрел 14' монитор фирмы Samsung. До сегодняшнего времени работал терпимо, но в этом году стало заметно "гашение" экрана. Выставляю уровень яркости на максимум, но этого явно не достаточно. Вот и хотел спросить я у вас, где в Интернет можно скачать утилиту, способную увеличивать яркость программно. Понимаю, что целесообразнее было ... подробнее
Впервые трое белорусских школьников примут участие во всемирном смотре научного и инженерного творчества юных Intel Isef'2000
2000/11‣разное :: тусовка
2 - 4 марта с.г. в 6-ой Политехнической гимназии г. Минска были подведены итоги регионального конкурса "БелЮниор'2000", впервые организованного в рамках Всемирного смотра научного и инженерного творчества юных Intel ISEF'2000. Более 350 старшеклассников из целого ряда городов Беларуси (Барановичей, Борисова, Бреста, Брянска, Витебска, Гродно, Минска) представили на БелЮниор'2000 свои научные творческие работы. В результате трое белорусских ... подробнее
По данным официального отчета, опубликованного Ассоциацией американских производителей электроники (American Electronics Association, AEA) и биржей NASDAQ, гд
2000/11‣del :: А знаете ли вы, что...?
По данным официального отчета, опубликованного Ассоциацией американских производителей электроники (American Electronics Association, AEA) и биржей NASDAQ, где котируются акции высокотехнологичных компаний, в 1999 г. в США объем экспорта продуктов высоких технологий достиг 181 млрд дол. То есть этот сектор экономики США стал самым крупным экспортером в стране. При этом объем импорта электроники в США составил в 1999 г. 220 млрд дол. В ... подробнее
Колобок
2000/11‣виртуальные радости :: КОМПАКТ-ДИСКОВ
Давным-давно, когда дискеты были большие, а программы маленькие, добрая фея Ада испекла Колобка. И сказала: "Катись, Колобок, по лесу, собирай первый в мире персональный компьютер из лесных жителей! Дам я тебе волшебство - каждый зверек в детальку превратится." И вот катится Колобок по лесу, а навстречу Ежик: - Колобок? Я тебя съем! - Не ешь меня, Ежик! - отвечает Колобок. - Лучше послушай, какое у меня к тебе деловое предложение - хочешь ... подробнее
XTEQ X - SETUP 5.5, или Тотальная перенастройка Windows 9x...
2000/11‣soft :: системные программы
Всем известно, что операционную систему Windows можно довольно-таки гибко настроить под конкретного пользователя. В этой статье я расскажу о программе, которая помогает менять такие настройки Винды, о которых Вы даже и не подозревали. Имя этой программки, как явствует из названия, - Xteq X-Setup. Ее интерфейс предельно прост, так что установить и разобраться с программкой проблем не составит. Сразу хочу предупредить: для установки ... подробнее
Wallpaper changer, или Меняем рисунок рабочего стола
2000/11‣soft :: системные программы
Рисунок на рабочем столе, какой бы он ни был, со временем надоедает, приходится лезть в Параметры рабочего стола и ставить другую картинку. Было бы прекрасно, если бы рисунок менялся каждый раз при загрузке компьютера или, скажем, через каждые полчаса работы компьютера. Wallpaper changer и делает всю эту грязную работу. WALLPAPER CHANGER - бесплатная программа для Windows 9x/NT, которая может менять заставку рабочего стола, поддерживает ... подробнее
МО: Тестирование
2000/11‣hard :: приводы
Судя по тому, что вы читаете эти строки, я могу сказать, что тема магнитооптики вам интересна. Как я и обещал, этот раз мы будем говорить о внутренних магнитооптических накопителях Fujitsu емкостью 1300 Мб. Начнем с того, что в первой части данной статьи, которую вы все могли видеть в КГ N№9, 2000, из-за обилия противоречивой информации в Интернет даже у самой Fujitsu, мною было допущено несколько неточностей, которые я хотел бы ... подробнее
Gigabyte GA-6WXM-e
2000/11‣hard :: mb

За и против интегрированных решений можно спорить бесконечно. В некоторых случаях материнские платы с интегрированными видео и звуком будут неуместными. Например, для игровой или развлекательной системы логичнее будет подобрать отдельные компоненты, чтобы в будущем можно было легко модернизировать систему. К тому же отдельные компоненты, как правило, значительно производительней и функциональней интегрированных. Впрочем, для интегрированных ... подробнее
Digidesign Digi 001
2000/11‣del :: Новости звука
Digidesign Digi 001 Компьютерная система Digidesign Digi 001 (995$) для Mac OS и Windows 98 (поддержка Windows 98 обещается в начале 2000 года) состоит из PCI платы и коммутационного блока. Аналоговых входов восемь, два из них (на разъемах XLR и на джеках) имеют микрофонные предусилители, регуляторы чувствительности, аттенюаторы (-26 дБ), пропускающие фильтры высоких частот (частота среза 60 Гц) и фантомное питание (48 В); остальные шесть (на ... подробнее
Интернет бизнес-клубы как главный двигатель прогресса
2000/11‣интернет :: разное
Вы не задумывались, почему многие бизнес-проекты в Интернет с грохотом проваливались, а другие - с маленьким начальным капиталом, стартовавшие позже, начинали быстро расти и захватывать рынок? В последнее время все больше бизнес-проектов, особенно в Интернет, развиваются как бизнес-клубы. Вы думаете, что не сталкивались с бизнес-клубами? Практически любой провайдер предлагает вам стать посредником по предоставлению доступа к Интернет, т.е. ... подробнее
Электронный бизнес в вопросах и ответах. Как создать собственный бизнес Глава 7
2000/11‣интернет :: продажи
Продолжение. Начало в КГ №№ 6, 7, 10 Глава 7. Обслуживание виртуальных магазинов. Почему на Интернет-страничках рано или поздно появляются виртуальные магазины? Руководство любого предприятия, пытающееся разместить информацию о себе в Интернет, приходит к идее размещения там информации о предлагаемых товарах и услугах, т.е. сначала на Интернет-страничке появляется информационный каталог товаров и услуг. Следующим этапом становится ... подробнее
Читатель интересуется (продолжение)
2000/11‣интернет :: разное
6 марта я получил множество восторженных писем примерно следующего содержания. Зашел сегодня на статистику, смотрю - БАА! В феврале у меня всего ~2500 очков было, - это по моим подсчетам примерно 20 баков, а тут у меня за февраль сразу около 7000 поинтов, и уже готовых к оплате ($53)! Я подумал, что это глюк Спедии и зашел в Detailed Report. Оказалось, что мне начислили ~4500 premier points (то есть премиальных очков)! За что?! Реферралов я ... подробнее
HomeWorld: Cataclysm
2000/11‣виртуальные радости :: нет данных

Разработчик: Barking Dog Studios, Ltd. Издатель: Sierra Studious. Официальная страница: http://sierrastudios.com/games/hwcataclysm/. Жанр: Strategy. Это должно было случиться. Игра, поразившая всех своим смелым шагом в стратегическое завтра, просто должна была обзавестись своим адд-оном. И, как это часто бывает, делает адд-он совершенно другая команда, купившая права у Relic. Barking Dog Studios (именно эта компания отвечает за ... подробнее
Summoner
2000/11‣виртуальные радости :: нет данных

Разработчик: Volition Incorporated Издатель: Electronic Arts Жанр: RPG Минимальные требования: P300, 64 Mb RAM, видео SVGA Некоторое время назад, спор о том, нужно ли восточное РПГ на РС, традиционно считавшееся в консервативных кругах компьютерного мира консольной ересью, был завершен. Элита обоих направлений смирилась с существованием позиции оппонентов, и полемика завершилась. Завершилась универсально: не нравится - не играй. Тот ... подробнее
Страшное-страшное будущее в великолепной трехмерной графике
2000/11‣виртуальные радости :: нет данных
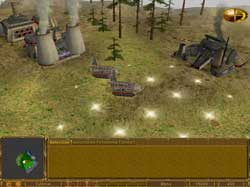
Название: EARTH 2150. Разработчик: TopWare Interactive. Издатель: SSI. Системные требования: P-200MMX, 32 Mb RAM, 4 Mb 3D Accelerator. Рекомендуется: P-II, 64 MB, 8 Mb 3D Accelerator. В чем, собственно, дело? Сюжет предстоящей нам стратегической мясорубки в реальном времени довольно "оригинален":). На земле в 21 веке разразилась Великая война, в которой человечество поставило себя на грань между полным уничтожением и адски сложной ... подробнее
Очередное завоевание галактики
2000/11‣виртуальные радости :: нет данных

Название: Imperium Galactica II. Разработчик: Digital Reality. Издатель: GT Interactive Software. Системные требования: P-233, 32 Mb RAM, 4MB 3D Accelerator. Рекомендовано: P-II-300, 64 Mb RAM, 16Mb 3D Accelerator. Мультиплейер: LAN, Internet Дата выхода: конец 2000 года. Отзвуки славы Master of Orion Давным-давно отгремели великие битвы между огромными галактическими империями в виртуальной вселенной Master of Orion. Многие ... подробнее
Гимн Porsche под дудку Electronic Arts
2000/11‣виртуальные радости :: нет данных

Название: Need For Speed: Porsche Unleashed. Разработчик: Electronic Arts. Издатель: Electronic Arts. Жанр: симулятор/аркада. Дата выхода: весна 2000. Никто, я думаю, не будет спорить с утверждением, что сериал Need for Speed от Electronic Arts является на данный момент самым популярным симулятором автогонок. Эта игра сочетает в себе изрядную долю аркадности с налетом реалистичности; лицензированные машины (от всего восьми в первом Need ... подробнее
Графика OpenGL: программирование на Фортране.
2000/11‣литература :: программирование
Бартеньев О. Графика OpenGL: программирование на Фортране. М.: ДИАЛОГ-МИФИ, 2000. - 368 с. Пособие посвящено одному из наиболее интересных разделов программирования - машинной графике. Предлагаемый материал содержит подробное описание возможностей графической библиотеки OpenGL для Windows, находящей применение в широком спектре приложений: в задачах САПР, системах дизайна, программах статистического анализа и математического моделирования ... подробнее
Графика OpenGL: программирование на Фортране
2000/11‣литература :: программирование
Бартеньев О. Графика OpenGL: программирование на Фортране. М.: ДИАЛОГ-МИФИ, 2000. - 368 с. Пособие посвящено одному из наиболее интересных разделов программирования - машинной графике. Предлагаемый материал содержит подробное описание возможностей графической библиотеки OpenGL для Windows, находящей применение в широком спектре приложений: в задачах САПР, системах дизайна, программах статистического анализа и математического моделирования ... подробнее
Большая энциклопедия живописи стран мира
2000/11‣виртуальные радости :: ОБЗОР КОМПАКТ-ДИСКОВ
Большая энциклопедия живописи стран мира Мы все становимся свидетелями возрождения отечественного рынка мультимедийных энциклопедий. Качественных энциклопедий, прошу заметить, не просто развлекательных, а еще и культурно-образовательных. После всплеска пиратства и последовавшего через год пресловутого "августовского финансового кризиса" отечественный рынок компьютерных энциклопедий с громким треском рухнул. Перестали появляться ... подробнее


